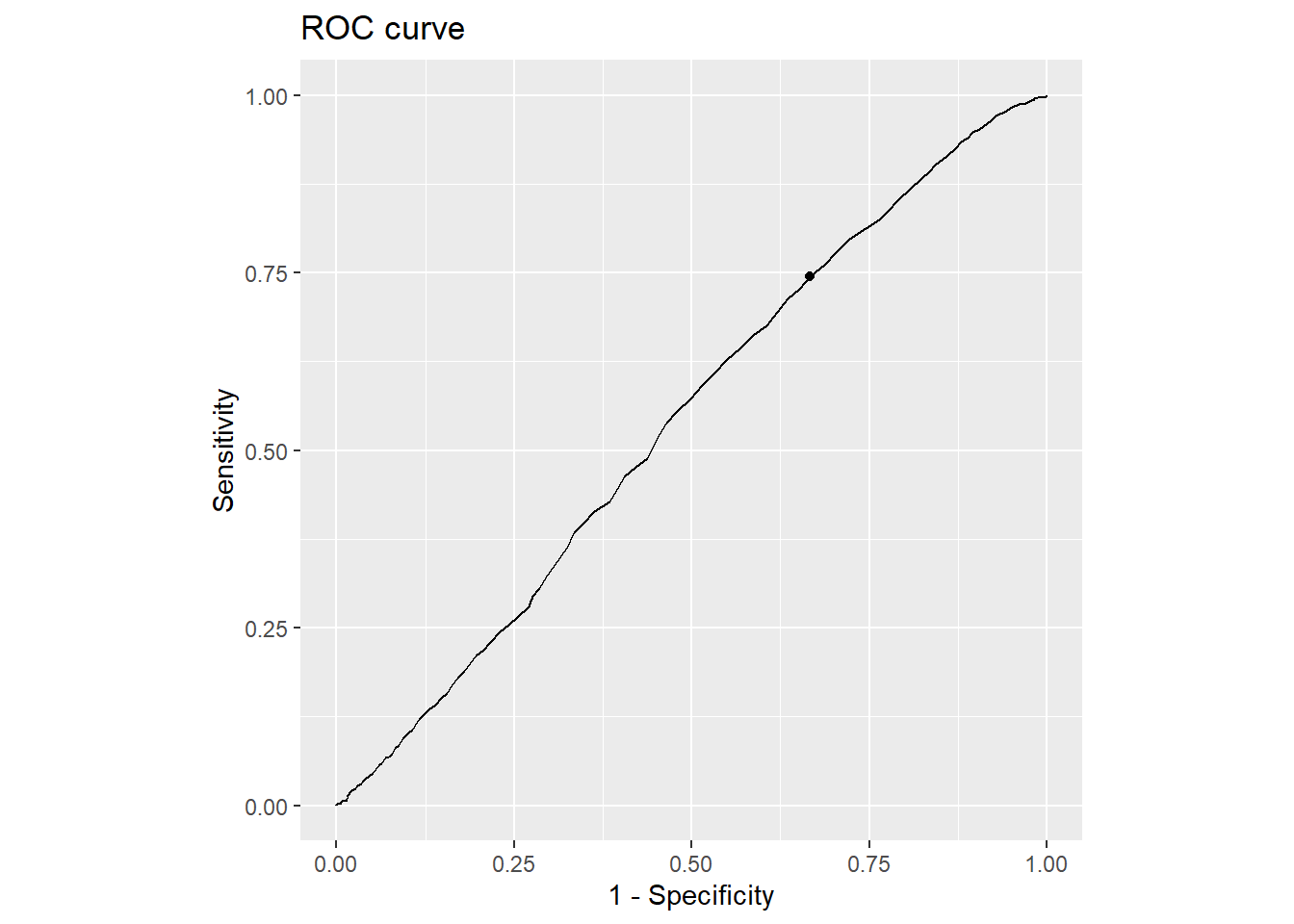We begin by importing data.
Code
df_data <-
readxl::read_xlsx("C:\\Dataset\\SBPDATA.xlsx") %>%
janitor::clean_names() %>%
select(
disease_class, a1_gender, sbp_0, sbp_6, sbp_12, sbp_18) %>%
mutate(
a1_gender = factor(
a1_gender,
levels = c(0,1),
labels = c("Female","Male")),
hpt = case_when(
str_detect(disease_class, "HPT") ~ "Yes",
TRUE ~ "No"),
dm = case_when(
str_detect(disease_class, "DM") ~ "Yes",
TRUE ~ "No")) %>%
select(hpt, dm, a1_gender, sbp_0) %>%
drop_na()
df_data %>% head()
# A tibble: 6 × 4
hpt dm a1_gender sbp_0
<chr> <chr> <fct> <dbl>
1 Yes No Female 139
2 Yes Yes Female 155
3 Yes No Female 109
4 Yes No Female 130
5 Yes No Female 124
6 Yes Yes Female 140
Next, we look at the distribution of systolic blood pressure for those with and without hypertension pressure.
Code
cut_one <-
df_data %>%
cutpointr::cutpointr(x = sbp_0, class = hpt)
Assuming the positive class is Yes
Assuming the positive class has higher x values
Code
Method: maximize_metric
Predictor: sbp_0
Outcome: hpt
Direction: >=
AUC n n_pos n_neg
0.7383 3285 2864 421
optimal_cutpoint sum_sens_spec acc sensitivity specificity tp fn fp tn
137 1.3715 0.6128 0.5876 0.7838 1683 1181 91 330
Predictor summary:
Data Min. 5% 1st Qu. Median Mean 3rd Qu. 95% Max. SD NAs
Overall 70 109 125 139 141.2003 155 180 230 22.21493 0
No 81 100 113 124 125.8385 135 160 208 18.26231 0
Yes 70 111 128 141 143.4584 157 181 230 21.84820 0
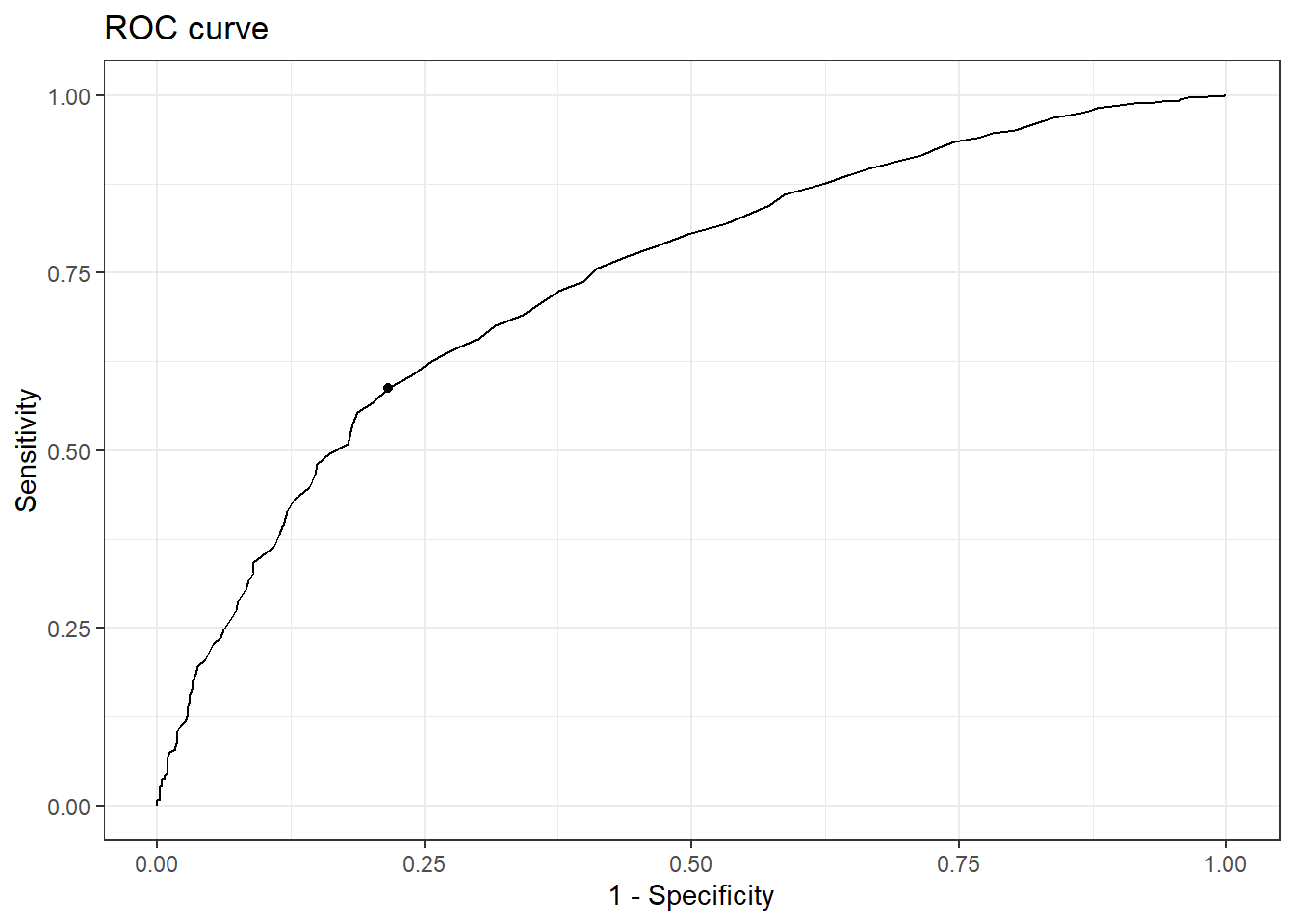
We then visualise the ROC curve.
Code
cut_one %>%
cutpointr::plot_roc() +
theme_bw()
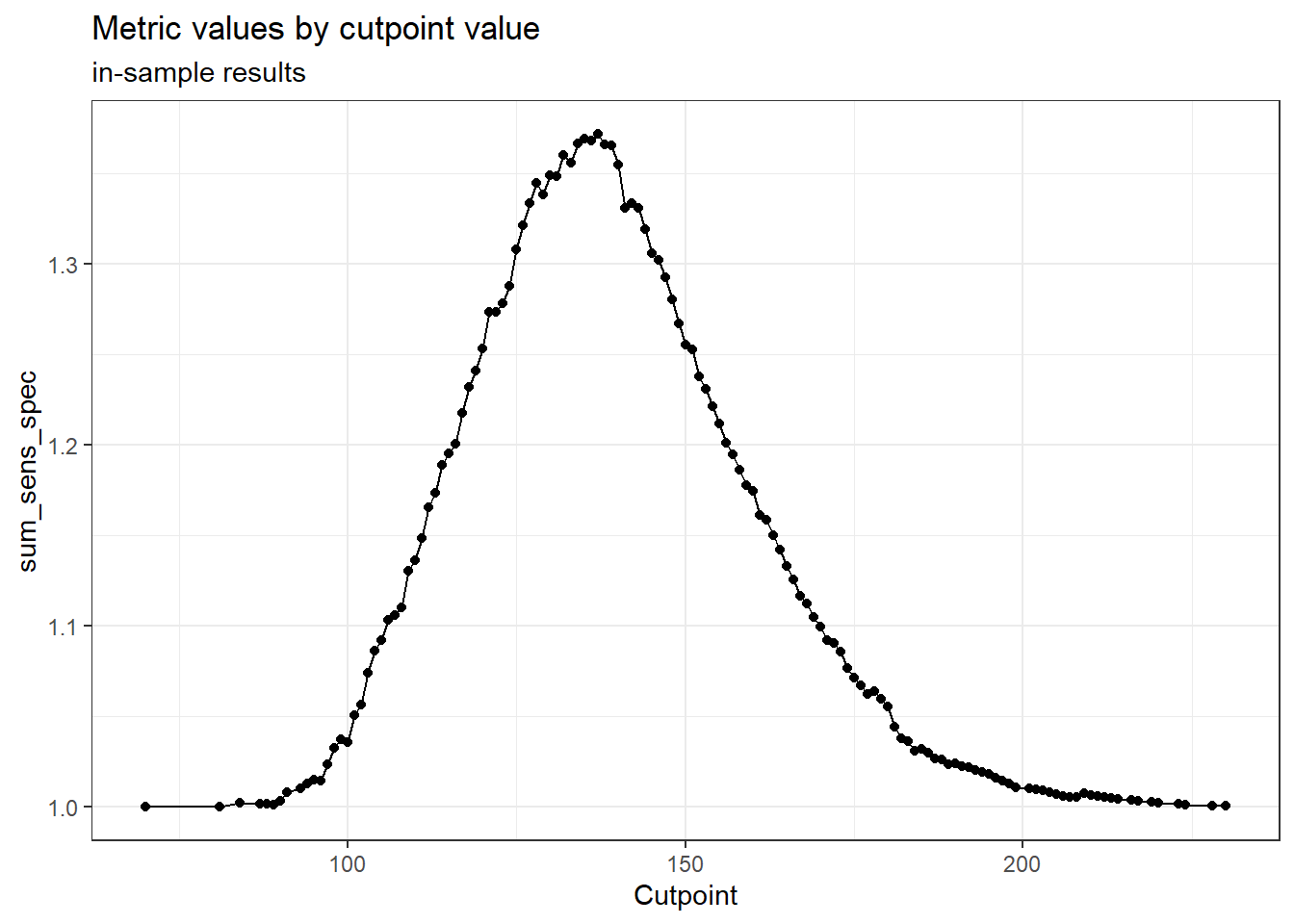
We can visualise the sensitivity _ specificity at all the cut-offs below.
Code
cut_one %>%
cutpointr::plot_metric(add_unsmoothed = T) +
theme_bw()
The analysis below can show multiple cut-off points, whereas we have only one here.
Code
cutoff_2 <-
cutpointr::cutpointr(
data = df_data,
x = sbp_0,
class = dm,
method = cutpointr::maximize_metric,
metric = cutpointr::sum_sens_spec,
break_ties = c)
Assuming the positive class is No
Assuming the positive class has higher x values
Code
Method: maximize_metric
Predictor: sbp_0
Outcome: dm
Direction: >=
AUC n n_pos n_neg
0.5432 3285 1861 1424
optimal_cutpoint sum_sens_spec acc sensitivity specificity tp fn fp tn
128 1.0789 0.5668 0.7453 0.3336 1387 474 949 475
Predictor summary:
Data Min. 5% 1st Qu. Median Mean 3rd Qu. 95% Max. SD NAs
Overall 70 109 125 139 141.2003 155 180 230 22.21493 0
No 70 111 127 140 142.4562 156 180 230 21.29190 0
Yes 81 106 123 136 139.5590 155 181 228 23.27191 0
Code
cutpointr::plot_roc(cutoff_2)
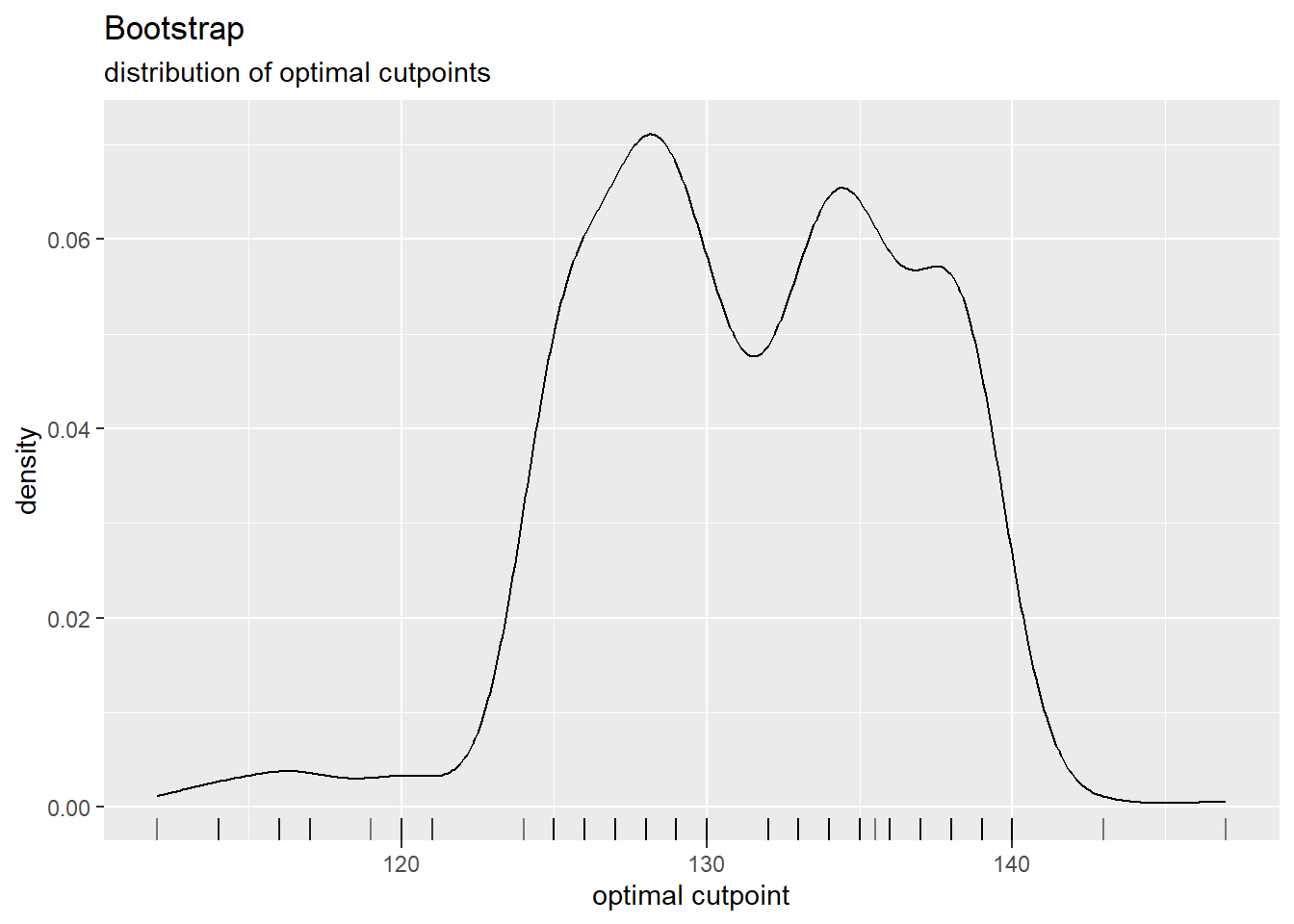
The confidence interval of the cutoff can be determined by bootstrapping as below:
Code
set.seed(999)
cutoff_3 <-
cutpointr::cutpointr(
data = df_data,
x = sbp_0,
class = dm,
boot_runs = 500)
Assuming the positive class is No
Assuming the positive class has higher x values
Code
Method: maximize_metric
Predictor: sbp_0
Outcome: dm
Direction: >=
Nr. of bootstraps: 500
AUC n n_pos n_neg
0.5432 3285 1861 1424
optimal_cutpoint sum_sens_spec acc sensitivity specificity tp fn fp tn
128 1.0789 0.5668 0.7453 0.3336 1387 474 949 475
Predictor summary:
Data Min. 5% 1st Qu. Median Mean 3rd Qu. 95% Max. SD NAs
Overall 70 109 125 139 141.2003 155 180 230 22.21493 0
No 70 111 127 140 142.4562 156 180 230 21.29190 0
Yes 81 106 123 136 139.5590 155 181 228 23.27191 0
Bootstrap summary:
Variable Min. 5% 1st Qu. Median Mean 3rd Qu. 95% Max.
optimal_cutpoint 112.00 125.00 128.00 132.00 131.36 135.62 139.00 147.00
AUC_b 0.51 0.53 0.54 0.54 0.54 0.55 0.56 0.58
AUC_oob 0.49 0.52 0.53 0.54 0.54 0.55 0.57 0.58
sum_sens_spec_b 1.05 1.07 1.08 1.09 1.09 1.10 1.11 1.14
sum_sens_spec_oob 1.00 1.03 1.05 1.06 1.06 1.08 1.10 1.13
acc_b 0.52 0.54 0.55 0.56 0.56 0.57 0.58 0.60
acc_oob 0.48 0.52 0.54 0.55 0.55 0.56 0.58 0.60
sensitivity_b 0.41 0.55 0.61 0.68 0.68 0.76 0.81 0.96
sensitivity_oob 0.37 0.53 0.59 0.67 0.67 0.75 0.80 0.94
specificity_b 0.10 0.27 0.33 0.41 0.40 0.49 0.54 0.66
specificity_oob 0.10 0.25 0.32 0.39 0.39 0.47 0.53 0.64
cohens_kappa_b 0.05 0.07 0.08 0.09 0.09 0.10 0.11 0.14
cohens_kappa_oob 0.00 0.03 0.05 0.07 0.06 0.08 0.10 0.14
SD NAs
5.30 0
0.01 0
0.01 0
0.01 0
0.02 0
0.01 0
0.02 0
0.10 0
0.10 0
0.10 0
0.10 0
0.01 0
0.02 0
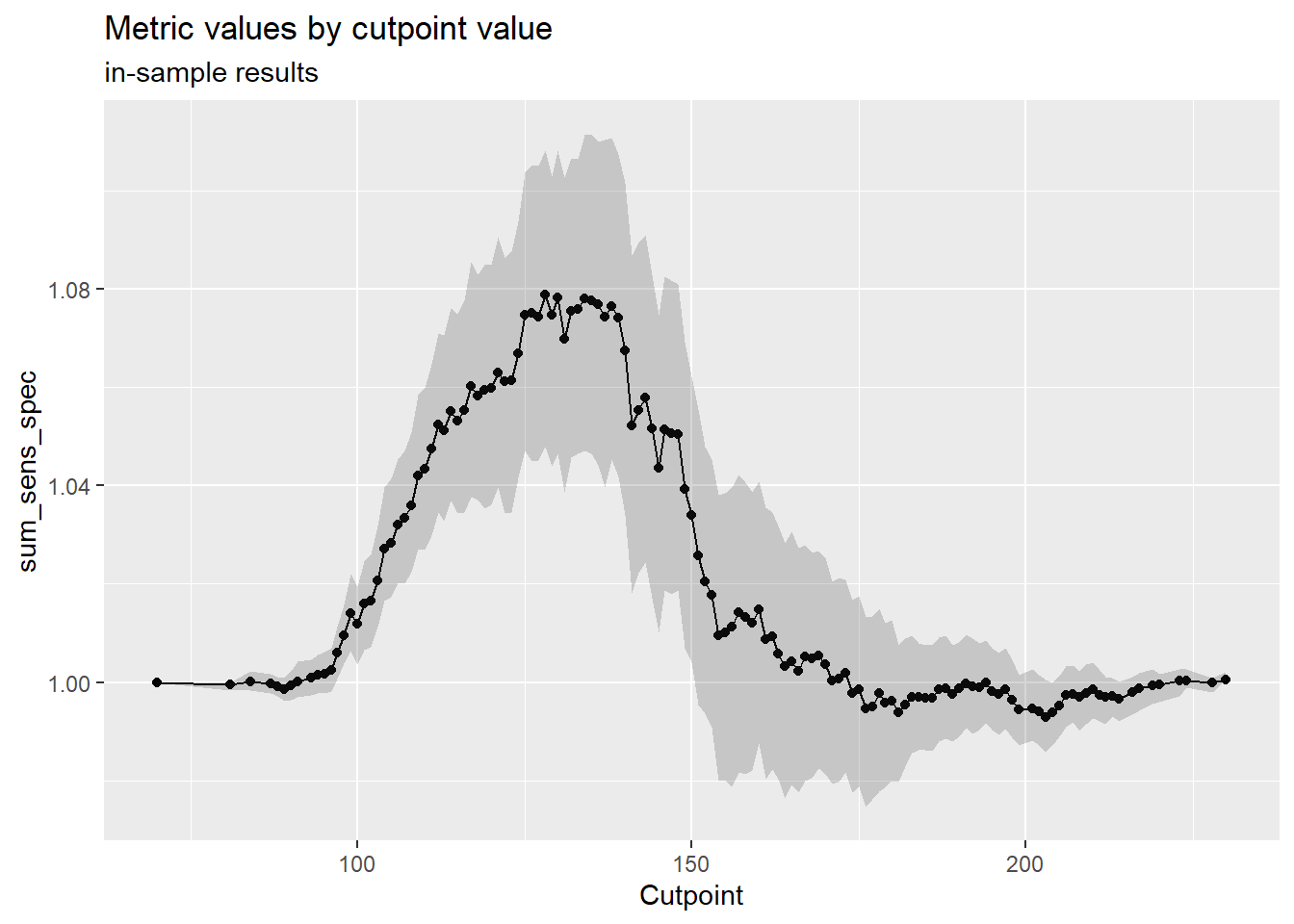
Code
cutpointr::plot_metric(cutoff_3)
Code
cutpointr::plot_cut_boot(cutoff_3)
Two different cutoffs could mean clustering. We, therefore, run cutoffs by sex to see
Code
set.seed(999)
cutoff_4 <-
cutpointr::cutpointr(
data = df_data,
x = sbp_0,
class = dm,
boot_runs = 500,
subgroup = a1_gender)
Assuming the positive class is No
Assuming the positive class has higher x values
We then summarise it.
Code
Method: maximize_metric
Predictor: sbp_0
Outcome: dm
Direction: >=
Subgroups: Female, Male
Nr. of bootstraps: 500
Subgroup: Female
--------------------------------------------------------------------------------
AUC n n_pos n_neg
0.5421 2515 1431 1084
optimal_cutpoint sum_sens_spec acc sensitivity specificity tp fn fp tn
130 1.0794 0.5622 0.703 0.3764 1006 425 676 408
Predictor summary:
Data Min. 5% 1st Qu. Median Mean 3rd Qu. 95% Max. SD NAs
Overall 70 108.0 125 139 140.7869 154 180 230 22.30675 0
No 70 110.5 127 140 141.9958 155 180 230 21.40570 0
Yes 89 105.0 123 136 139.1910 154 180 228 23.35758 0
Bootstrap summary:
Variable Min. 5% 1st Qu. Median Mean 3rd Qu. 95% Max.
optimal_cutpoint 112.00 117.00 126.00 130.00 129.33 133.00 140.00 146.00
AUC_b 0.51 0.52 0.53 0.54 0.54 0.55 0.56 0.58
AUC_oob 0.50 0.52 0.53 0.54 0.54 0.55 0.57 0.59
sum_sens_spec_b 1.05 1.06 1.08 1.09 1.09 1.10 1.11 1.15
sum_sens_spec_oob 0.99 1.02 1.04 1.06 1.06 1.08 1.10 1.13
acc_b 0.52 0.54 0.56 0.57 0.57 0.58 0.59 0.61
acc_oob 0.48 0.51 0.54 0.56 0.55 0.57 0.58 0.60
sensitivity_b 0.42 0.53 0.65 0.72 0.71 0.78 0.90 0.95
sensitivity_oob 0.38 0.51 0.62 0.71 0.70 0.76 0.89 0.96
specificity_b 0.11 0.18 0.31 0.37 0.38 0.45 0.56 0.66
specificity_oob 0.09 0.16 0.30 0.36 0.36 0.43 0.54 0.65
cohens_kappa_b 0.05 0.06 0.08 0.09 0.09 0.10 0.12 0.15
cohens_kappa_oob -0.01 0.02 0.04 0.06 0.06 0.08 0.10 0.14
SD NAs
6.30 0
0.01 0
0.02 0
0.02 0
0.02 0
0.02 0
0.02 0
0.11 0
0.11 0
0.11 0
0.11 0
0.02 0
0.02 0
Subgroup: Male
--------------------------------------------------------------------------------
AUC n n_pos n_neg
0.5486 770 430 340
optimal_cutpoint sum_sens_spec acc sensitivity specificity tp fn fp tn
136 1.1056 0.561 0.6233 0.4824 268 162 176 164
Predictor summary:
Data Min. 5% 1st Qu. Median Mean 3rd Qu. 95% Max. SD NAs
Overall 81 110 127 139 142.5506 157 182.00 220 21.87227 0
No 88 113 129 141 143.9884 159 181.10 210 20.86011 0
Yes 81 108 125 136 140.7324 157 182.05 220 22.99138 0
Bootstrap summary:
Variable Min. 5% 1st Qu. Median Mean 3rd Qu. 95% Max.
optimal_cutpoint 113.00 124.00 134.00 136.00 134.62 138.00 139.00 163.00
AUC_b 0.49 0.52 0.53 0.55 0.55 0.56 0.58 0.62
AUC_oob 0.46 0.50 0.53 0.55 0.55 0.57 0.60 0.63
sum_sens_spec_b 1.04 1.07 1.09 1.12 1.12 1.14 1.18 1.22
sum_sens_spec_oob 0.93 1.00 1.04 1.08 1.08 1.11 1.15 1.20
acc_b 0.48 0.54 0.56 0.57 0.57 0.58 0.60 0.63
acc_oob 0.45 0.51 0.53 0.55 0.55 0.57 0.59 0.63
sensitivity_b 0.24 0.55 0.59 0.63 0.65 0.69 0.85 0.96
sensitivity_oob 0.15 0.52 0.57 0.62 0.63 0.67 0.84 0.96
specificity_b 0.11 0.24 0.43 0.49 0.46 0.53 0.57 0.87
specificity_oob 0.08 0.22 0.40 0.47 0.44 0.51 0.56 0.79
cohens_kappa_b 0.05 0.07 0.09 0.12 0.12 0.14 0.18 0.22
cohens_kappa_oob -0.08 0.00 0.05 0.08 0.08 0.11 0.15 0.20
SD NAs
4.89 0
0.02 0
0.03 0
0.03 0
0.04 0
0.02 0
0.02 0
0.09 0
0.10 0
0.10 0
0.10 0
0.03 0
0.05 0
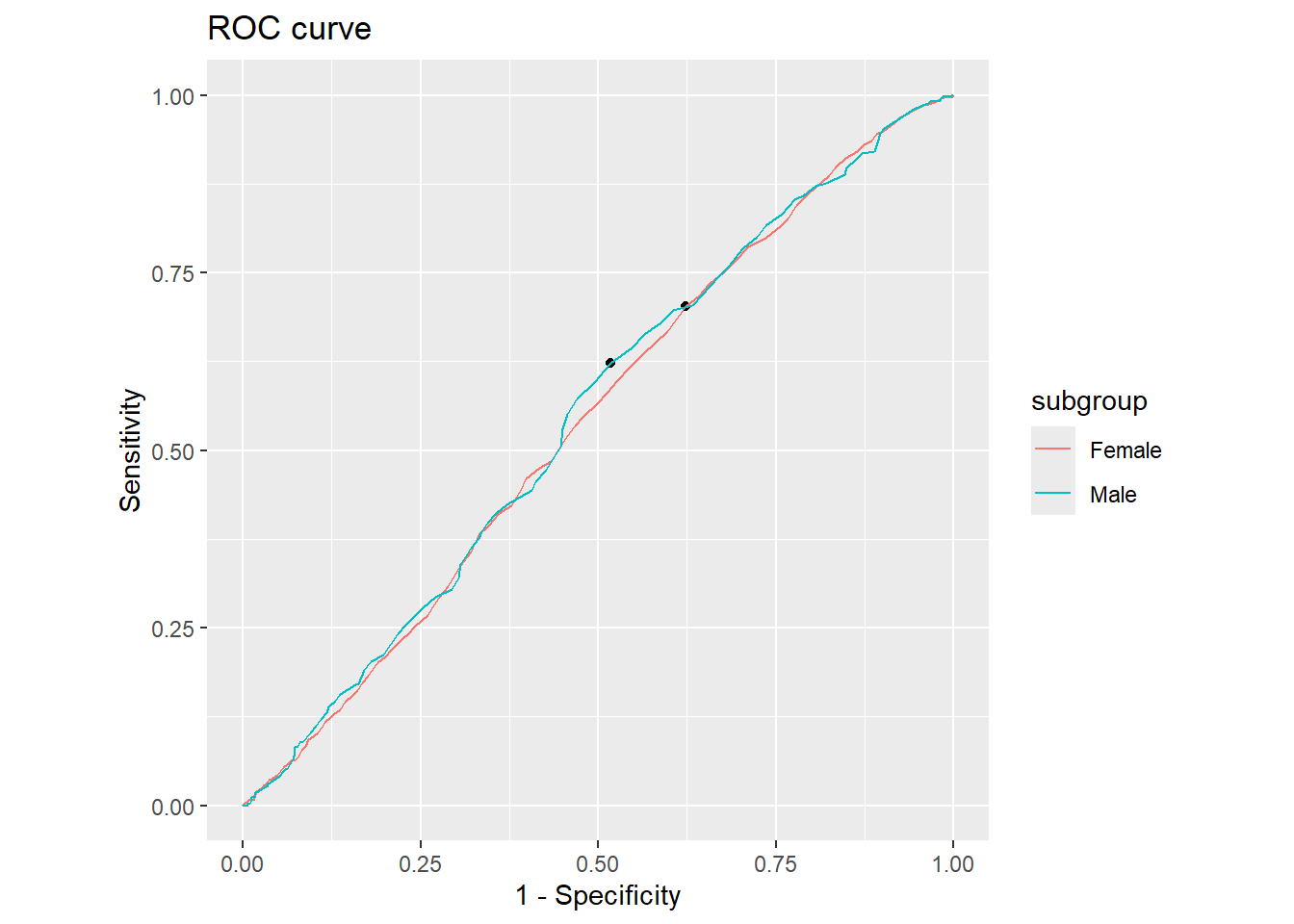
And then plot it
Code
cutpointr::plot_roc(cutoff_4)
And the we determine the cut-offs
Code
cutpointr::plot_metric(cutoff_4)
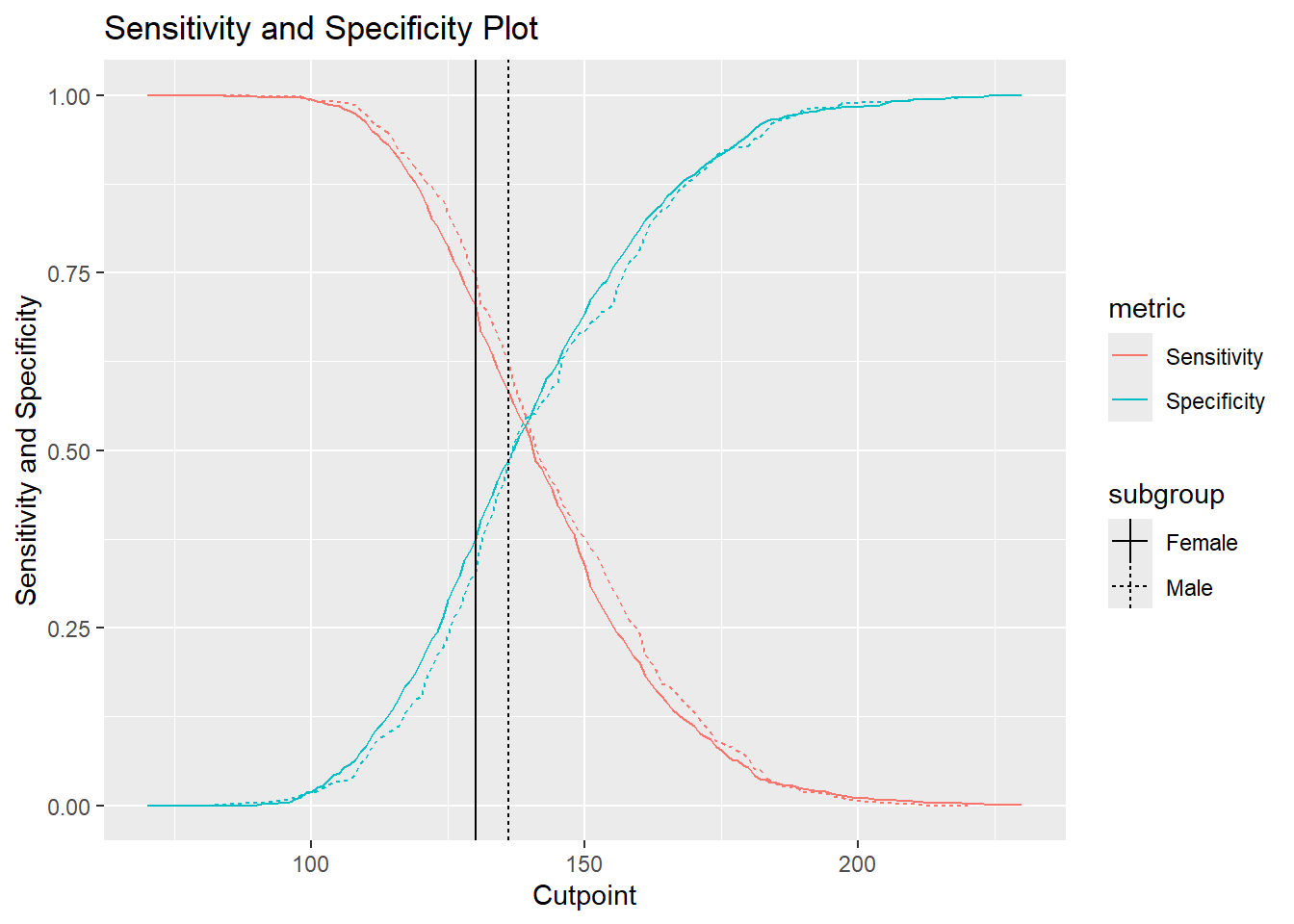
Multiple plot is a single command
Code
cutoff_4 %>%
cutpointr::plot_sensitivity_specificity()
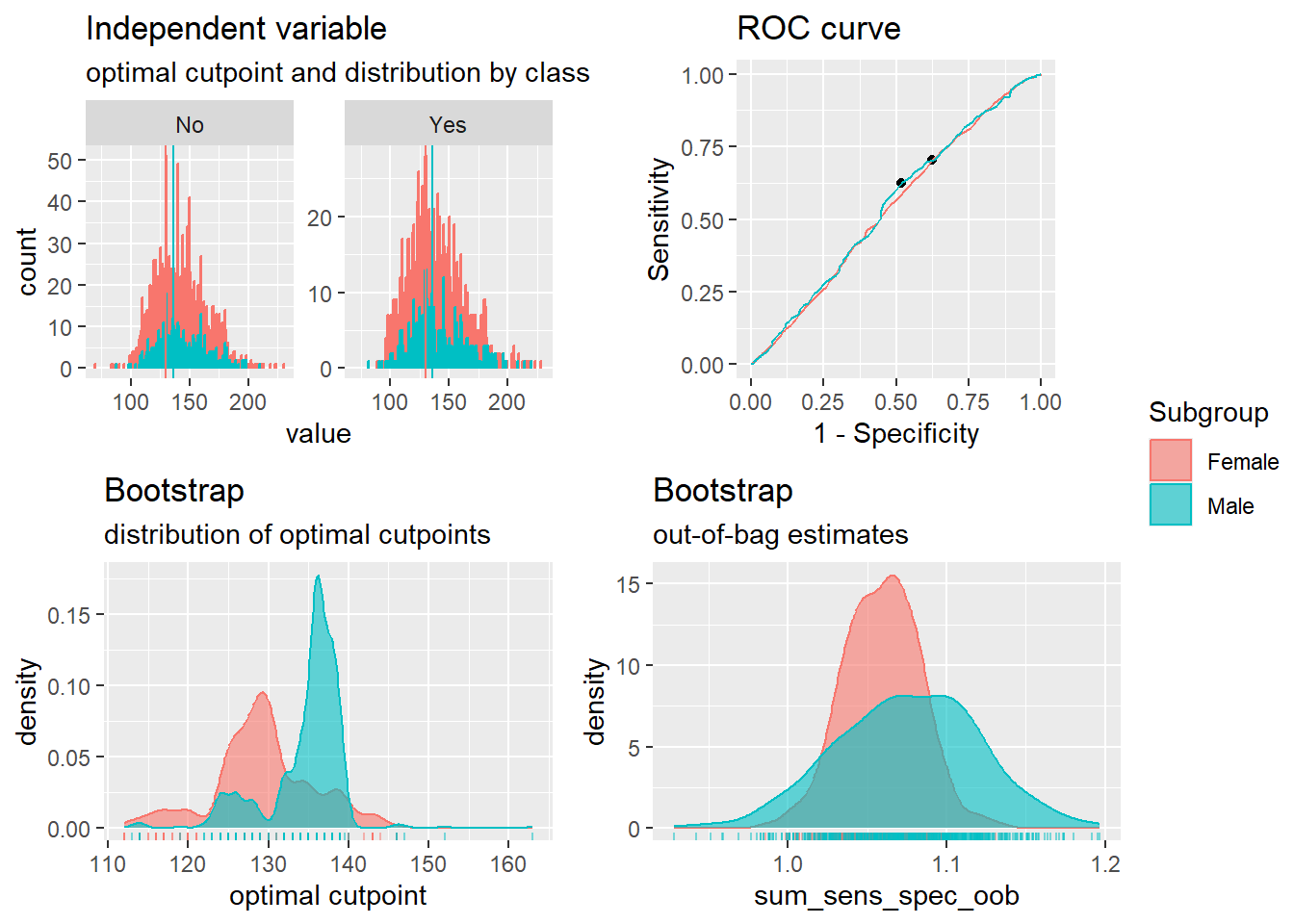
And even more
Code
cutoff_4 %>%
cutpointr::plot_precision_recall()