Acquiring the data
We begin by reading the data. Here we use the data from the Carotid Intima dataset
Code
<- dget ("C:/Dataset/cint_data_clean" )%>% select (cca_0, sex, ageyrs, resid, hba1c, tobacco, alcohol, bmi, %>% filter (! is.na (totchol), ! is.na (ldl)) %>% mutate (trig = if_else (trig > 40 , trig/ 10 , trig, missing = NULL ))
Next, we summarize the data
Code
%>% :: dfSummary (graph.col = F)
Data Frame Summary
dat
Dimensions: 702 x 15
Duplicates: 4
-------------------------------------------------------------------------------------
No Variable Stats / Values Freqs (% of Valid) Valid Missing
---- ----------- ------------------------- --------------------- ---------- ---------
1 cca_0 Mean (sd) : 0.9 (0.2) 40 distinct values 702 0
[numeric] min < med < max: (100.0%) (0.0%)
0.5 < 0.8 < 1.6
IQR (CV) : 0.2 (0.2)
2 sex 1. Female 545 (77.6%) 702 0
[factor] 2. Male 157 (22.4%) (100.0%) (0.0%)
3 ageyrs Mean (sd) : 44.3 (9) 46 distinct values 702 0
[numeric] min < med < max: (100.0%) (0.0%)
26 < 43 < 75
IQR (CV) : 12 (0.2)
4 resid 1. Rural 24 ( 3.4%) 702 0
[factor] 2. Periurban 174 (24.8%) (100.0%) (0.0%)
3. Urban 504 (71.8%)
5 hba1c Mean (sd) : 5.4 (1) 56 distinct values 702 0
[numeric] min < med < max: (100.0%) (0.0%)
3.1 < 5.3 < 15.5
IQR (CV) : 0.8 (0.2)
6 tobacco 1. No 657 (93.6%) 702 0
[factor] 2. Yes 45 ( 6.4%) (100.0%) (0.0%)
7 alcohol 1. No 458 (65.2%) 702 0
[factor] 2. Yes 244 (34.8%) (100.0%) (0.0%)
8 bmi Mean (sd) : 26.6 (5.6) 582 distinct values 702 0
[numeric] min < med < max: (100.0%) (0.0%)
13.3 < 26.1 < 45.3
IQR (CV) : 7.7 (0.2)
9 whratio Mean (sd) : 0.9 (0.1) 456 distinct values 702 0
[numeric] min < med < max: (100.0%) (0.0%)
0.6 < 0.9 < 1.2
IQR (CV) : 0.1 (0.1)
10 totchol Mean (sd) : 5.1 (1.3) 73 distinct values 702 0
[numeric] min < med < max: (100.0%) (0.0%)
1.1 < 5 < 11.1
IQR (CV) : 1.7 (0.3)
11 ldl Mean (sd) : 3.2 (1.1) 59 distinct values 702 0
[numeric] min < med < max: (100.0%) (0.0%)
0 < 3.1 < 8.1
IQR (CV) : 1.4 (0.3)
12 hdl Mean (sd) : 1.4 (0.5) 31 distinct values 702 0
[numeric] min < med < max: (100.0%) (0.0%)
0.3 < 1.3 < 4.4
IQR (CV) : 0.6 (0.4)
13 trig Mean (sd) : 1.4 (0.9) 227 distinct values 702 0
[numeric] min < med < max: (100.0%) (0.0%)
0.3 < 1.2 < 10.7
IQR (CV) : 0.8 (0.7)
14 sbp Mean (sd) : 125 (23.9) 118 distinct values 702 0
[numeric] min < med < max: (100.0%) (0.0%)
66 < 121 < 231
IQR (CV) : 28 (0.2)
15 dbp Mean (sd) : 79.5 (14.1) 71 distinct values 702 0
[numeric] min < med < max: (100.0%) (0.0%)
43 < 79 < 135
IQR (CV) : 19 (0.2)
-------------------------------------------------------------------------------------
Linear regression with a single continuous variable
We begin by looking at the relationship between the dependent and independent variables
Code
%>% ggplot (aes (x = ageyrs, y = cca_0)) + geom_point () + geom_smooth (method = "lm" , formula = y~ x) + labs (x = "Age in years" , y = "Common Carotid Intima thickness" ,title = "Relationship between CCA and Age of patient" ) + theme_classic ()
Since the relationship between the two looks linear we will go on to fit the model
Code
.1 <- lm (cca_0 ~ ageyrs, data = dat)
Next w,e summarise the model, extract the coefficients and confidence intervals with the help of the flextable package.
Code
.1 %>% flextable:: as_flextable ()
Estimate
Standard Error
t value
Pr(>|t|)
(Intercept)
0.628
0.029
21.988
0.0000
***
ageyrs
0.005
0.001
8.381
0.0000
***
Signif. codes: 0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05
Residual standard error: 0.1511 on 700 degrees of freedom
Multiple R-squared: 0.0912, Adjusted R-squared: 0.0899
F-statistic: 70.25 on 700 and 1 DF, p-value: 0.0000
Next, we extract some regression analysis stats required for the regression diagnostics
Code
tibble (resid = residuals (lm.1 ), fits = fitted (lm.1 ), st.resid = rstandard (lm.1 ),cookd = cooks.distance (lm.1 ),covr = covratio (lm.1 ),hatv = hatvalues (lm.1 ),dfit = dffits (lm.1 ),dfbeta1 = dfbeta (lm.1 )[,2 ]) %>% arrange (desc (cookd)) %>% round (5 ) %>% slice (1 : 10 ) %>% :: kable ()
0.40242
0.97258
2.67540
0.03210
0.99127
0.00889
0.25449
0.00015
0.52507
0.92493
3.48188
0.02314
0.97212
0.00380
0.21685
0.00011
-0.25435
1.00435
-1.69521
0.02018
1.00862
0.01385
-0.20119
-0.00012
0.71213
0.88787
4.71760
0.02012
0.94181
0.00180
0.20372
0.00006
0.53625
0.81375
3.55451
0.01868
0.96985
0.00295
0.19491
-0.00009
0.34330
0.95670
2.28006
0.01800
0.99487
0.00688
0.19033
0.00011
0.19948
1.02552
1.33222
0.01614
1.01593
0.01786
0.17975
0.00011
-0.24376
0.99376
-1.62316
0.01608
1.00748
0.01206
-0.17953
-0.00011
0.35389
0.94611
2.34901
0.01585
0.99279
0.00571
0.17864
0.00010
-0.25287
0.97787
-1.68180
0.01375
1.00445
0.00963
-0.16604
-0.00010
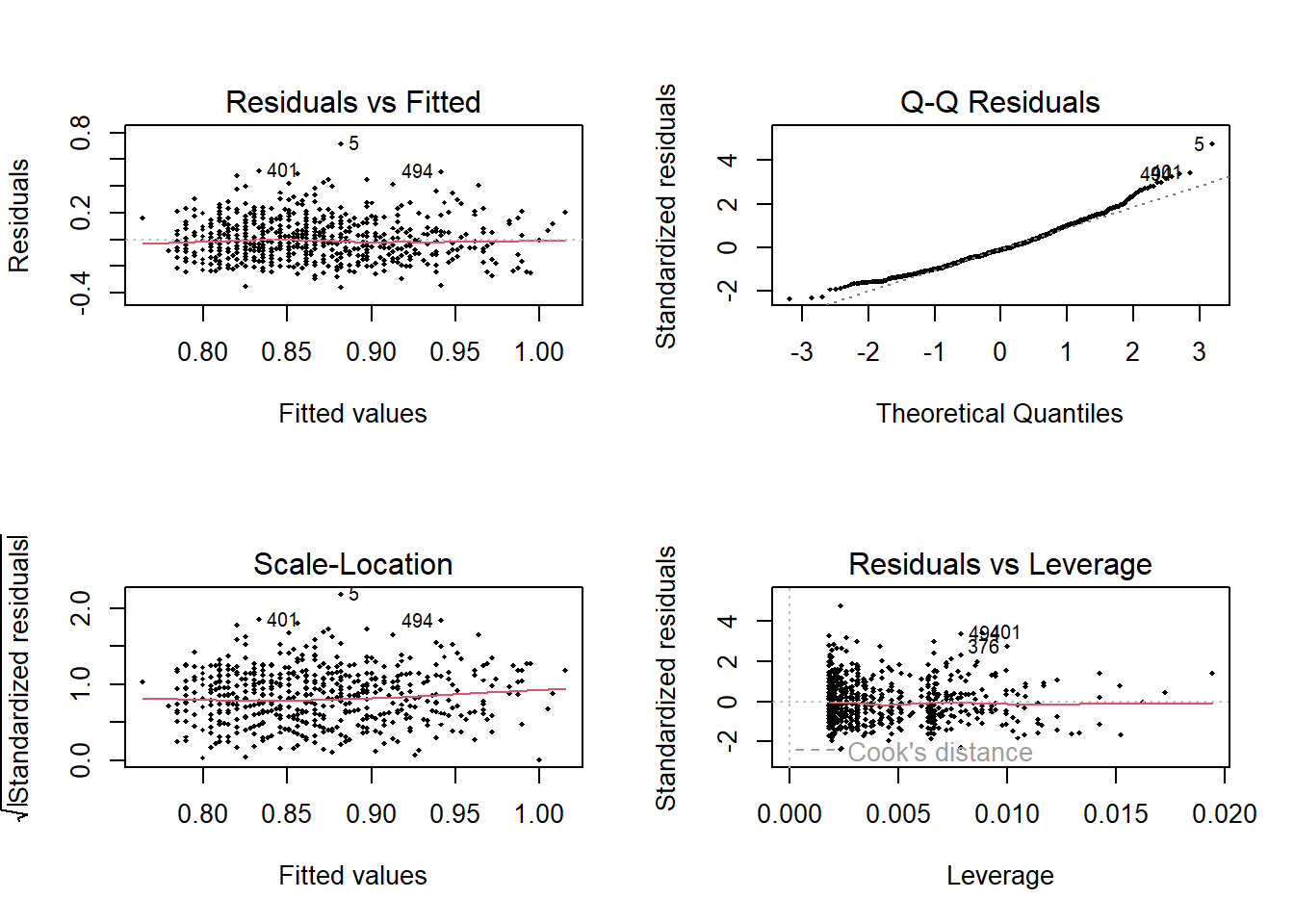
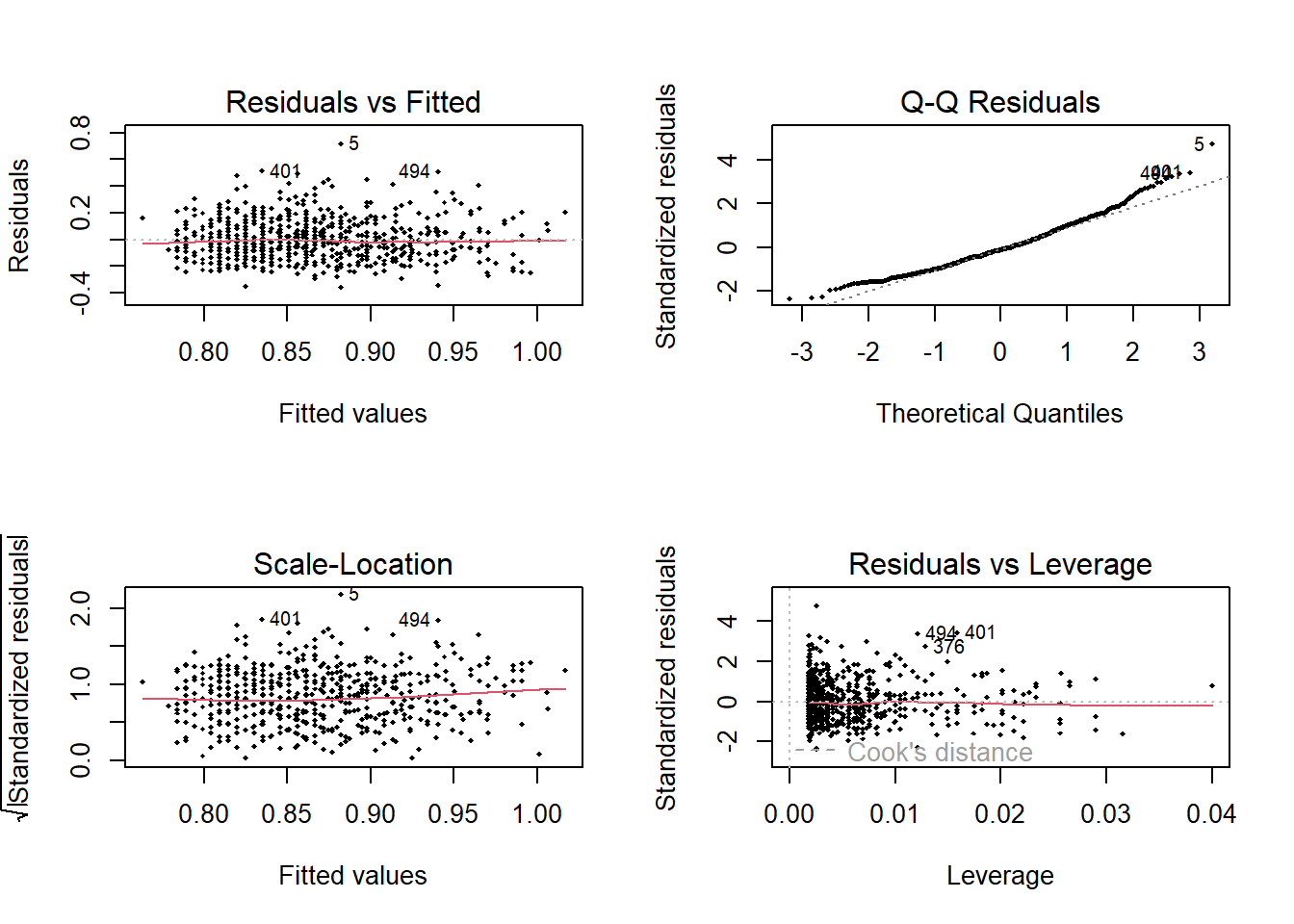
And then plot the regression diagnostic graphs
Code
<- par (mfrow = c (2 ,2 ))plot (lm.1 , pch = 18 , cex= .5 )
Code
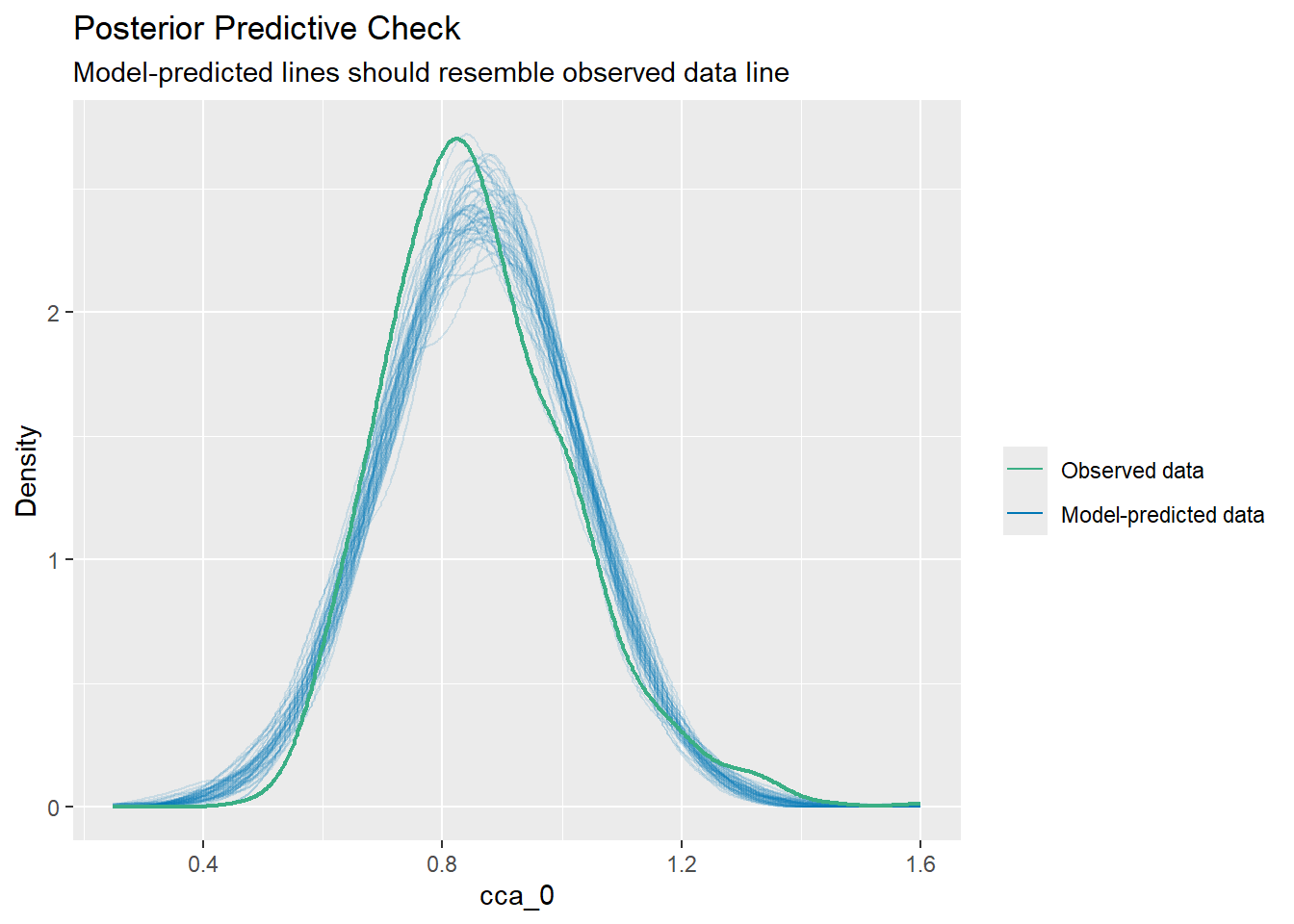
Below we formally check the model assumption with the performance package. First the normality of the residuals
Code
:: check_predictions (lm.1 )
Warning: Maximum value of original data is not included in the
replicated data.
Model may not capture the variation of the data.
Code
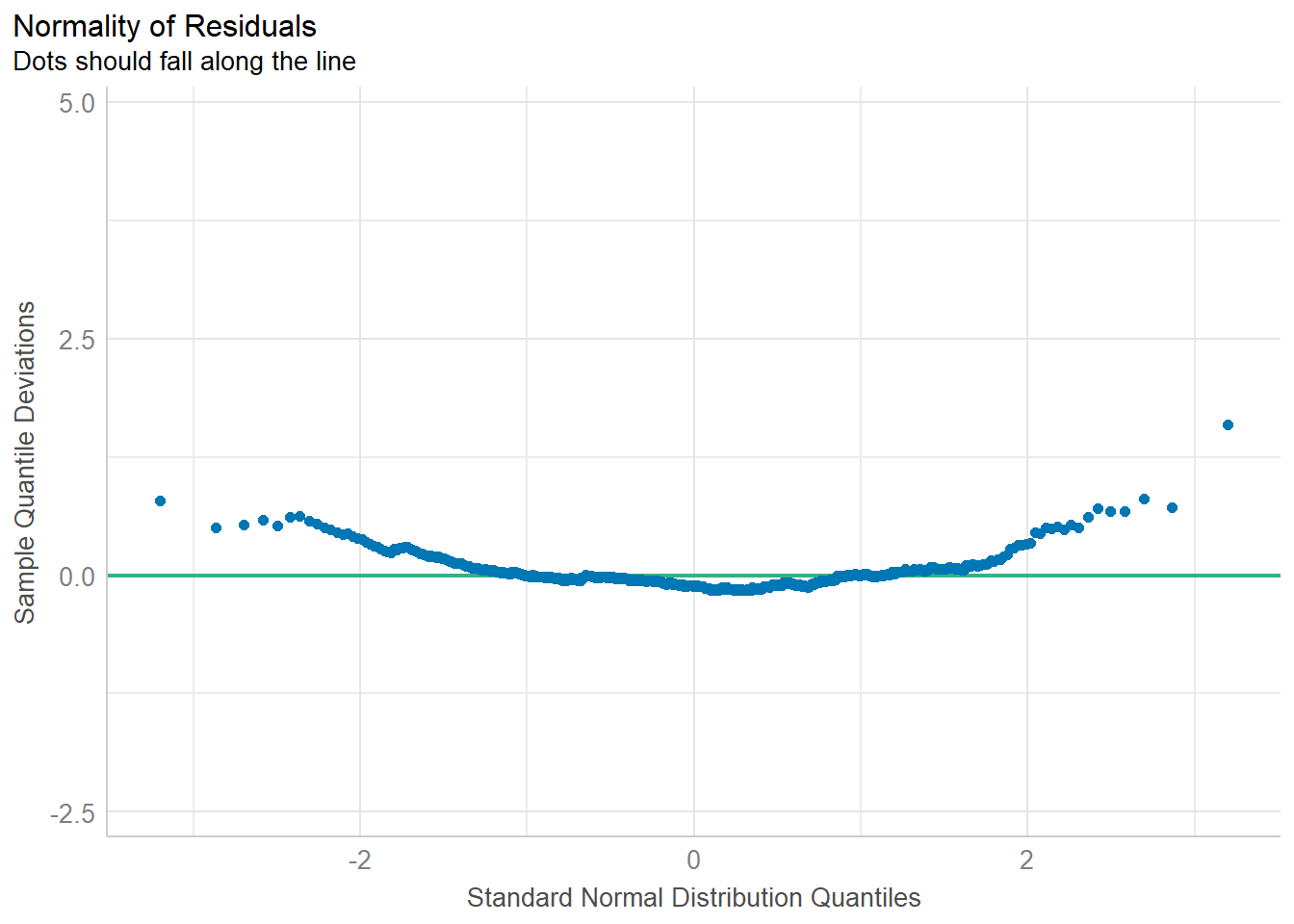
:: check_normality (lm.1 )
Warning: Non-normality of residuals detected (p < .001).
Code
:: check_normality (lm.1 ) %>% plot ()
For confidence bands, please install `qqplotr`.
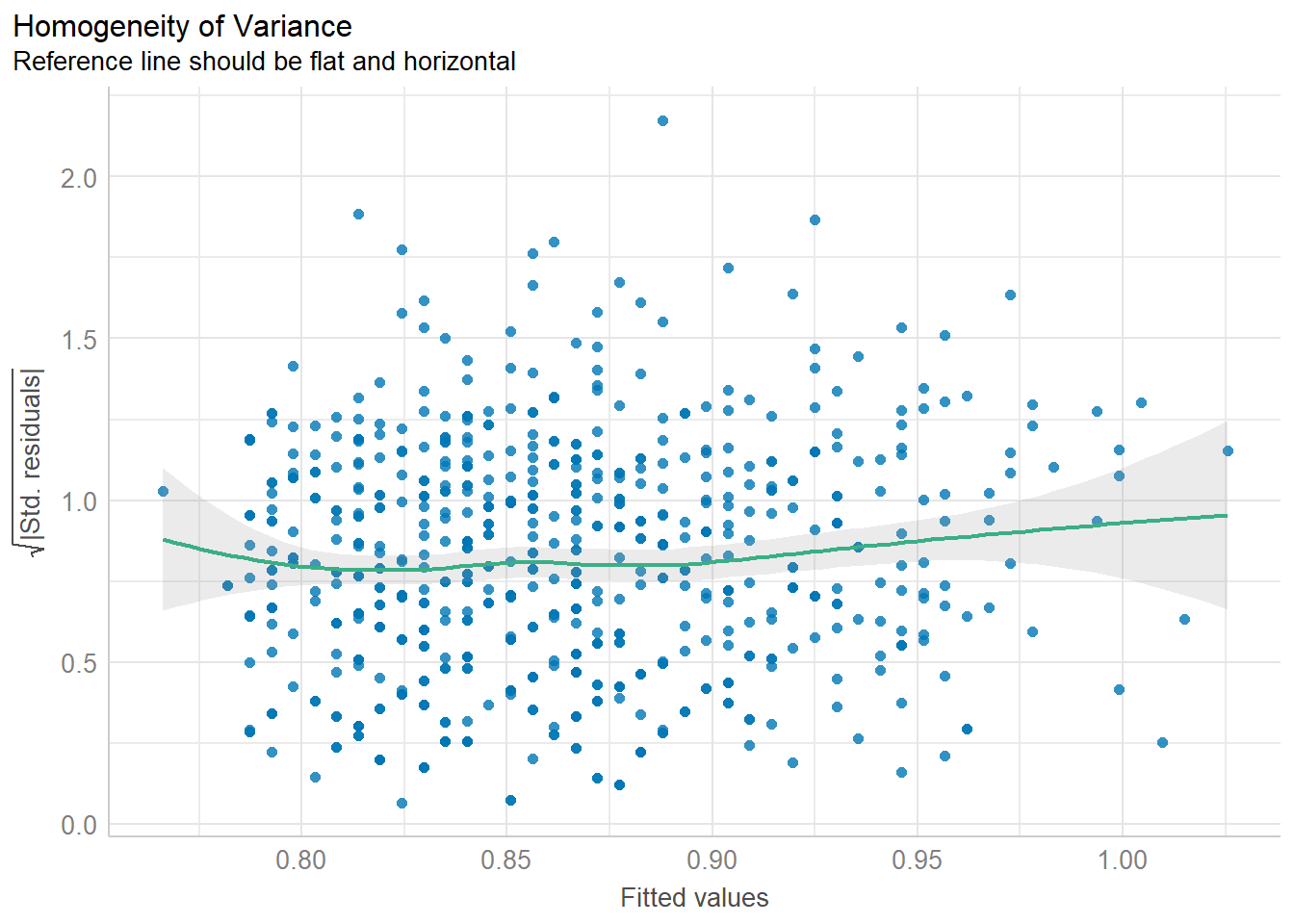
Next heteroscedasticity
Code
:: check_heteroscedasticity (lm.1 )
Warning: Heteroscedasticity (non-constant error variance) detected (p = 0.018).
Code
:: check_heteroscedasticity (lm.1 ) %>% plot ()
Code
:: check_distribution (lm.1 )
# Distribution of Model Family
Predicted Distribution of Residuals
Distribution Probability
normal 34%
beta 19%
cauchy 16%
Predicted Distribution of Response
Distribution Probability
inverse-gamma 28%
gamma 22%
beta 16%
Code
:: check_distribution (lm.1 ) %>% plot ()
Linear regression with one continuous and one categorical predictor
Code
.2 <- lm (cca_0 ~ ageyrs + sex, data = dat).2 %>% summary ()
Call:
lm(formula = cca_0 ~ ageyrs + sex, data = dat)
Residuals:
Min 1Q Median 3Q Max
-0.35690 -0.11033 -0.01512 0.08711 0.71810
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.6301958 0.0285622 22.064 < 2e-16 ***
ageyrs 0.0051368 0.0006377 8.056 3.42e-15 ***
sexMale 0.0234025 0.0138148 1.694 0.0907 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1509 on 699 degrees of freedom
Multiple R-squared: 0.09491, Adjusted R-squared: 0.09233
F-statistic: 36.65 on 2 and 699 DF, p-value: 7.294e-16
And then plot the diagnostics
Code
<- par (mfrow = c (2 ,2 )).2 %>% plot (pch = 18 , cex= .5 )
Code
Further, we plot the marginal plot for the various sexes
Code
%>% ggplot (aes (x = ageyrs, y = cca_0, col = sex)) + geom_smooth (formula = y~ x, method = "lm" ) + geom_point () + labs (x = "Age in years" , y = "CCA" , title = "CCA vrs Age for each sex" ) + theme_bw ()
Linear regression with one continuous and one categorical predictor with interaction
Code
.3 <- lm (cca_0 ~ ageyrs* sex, data = dat).3 %>% summary ()
Call:
lm(formula = cca_0 ~ ageyrs * sex, data = dat)
Residuals:
Min 1Q Median 3Q Max
-0.35711 -0.10997 -0.01482 0.08664 0.71789
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.6284770 0.0330494 19.016 < 2e-16 ***
ageyrs 0.0051762 0.0007429 6.968 7.45e-12 ***
sexMale 0.0303114 0.0681101 0.445 0.656
ageyrs:sexMale -0.0001503 0.0014510 -0.104 0.918
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.151 on 698 degrees of freedom
Multiple R-squared: 0.09493, Adjusted R-squared: 0.09104
F-statistic: 24.4 on 3 and 698 DF, p-value: 5.025e-15
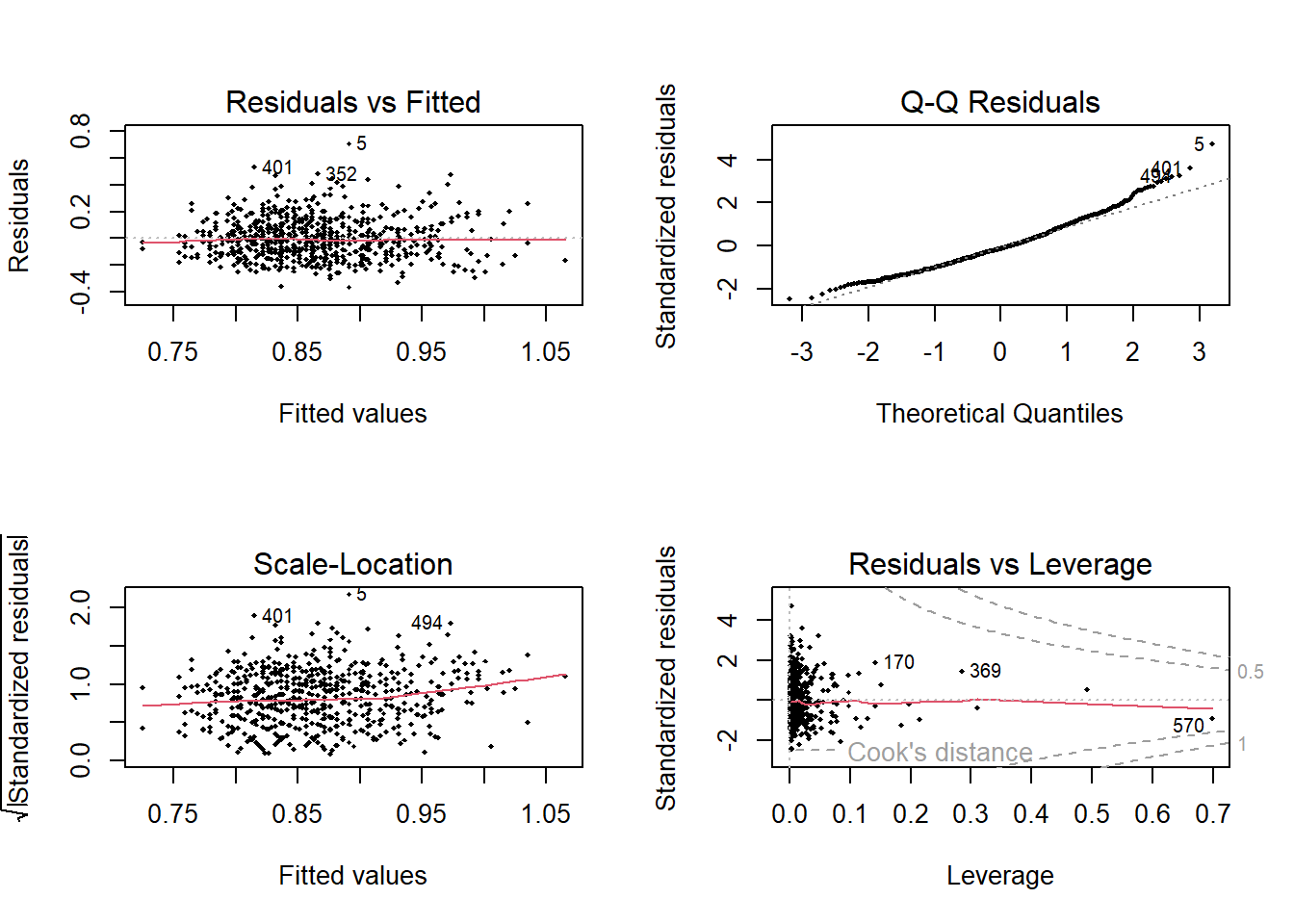
And then plot the diagnostics
Code
<- par (mfrow = c (2 ,2 )).3 %>% plot (pch = 18 , cex= .5 )
Code
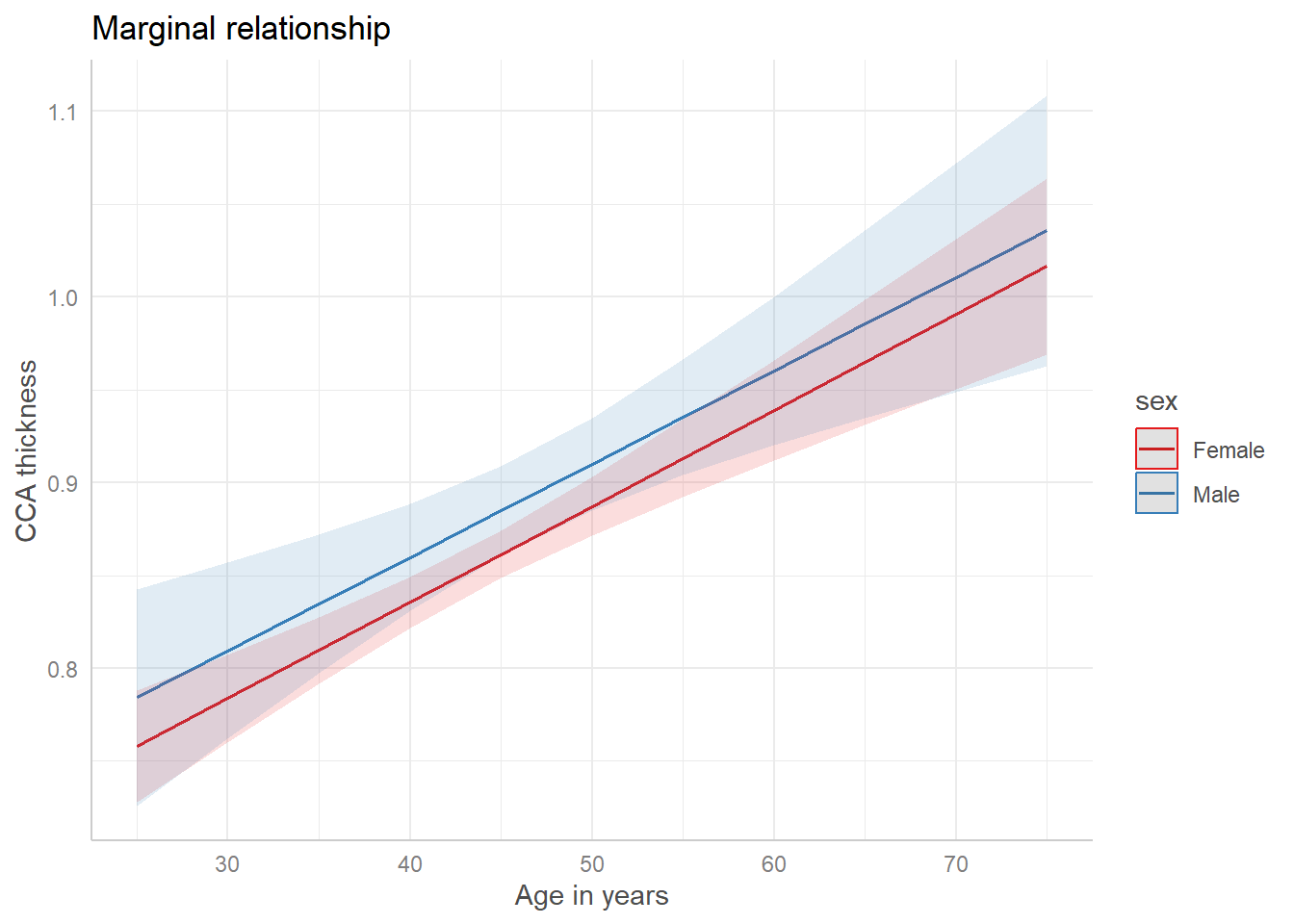
Next, we make a plot of the marginal effects after
Code
.3 <- :: ggpredict (lm.3 , terms = c ("ageyrs" , "sex" )).3 %>% plot () + labs (x = "Age in years" , y = "CCA thickness" , title = "Marginal relationship" )
Linear regression with one continuous and two categorical predictors with interaction
Code
.4 <- lm (cca_0 ~ ageyrs* sex* resid, data = dat).4 %>% summary ()
Call:
lm(formula = cca_0 ~ ageyrs * sex * resid, data = dat)
Residuals:
Min 1Q Median 3Q Max
-0.36621 -0.10171 -0.01644 0.08202 0.70879
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.434224 0.155773 2.788 0.00546 **
ageyrs 0.010017 0.003277 3.057 0.00232 **
sexMale -1.476681 1.361101 -1.085 0.27834
residPeriurban 0.171485 0.167778 1.022 0.30710
residUrban 0.213439 0.160840 1.327 0.18494
ageyrs:sexMale 0.034164 0.031289 1.092 0.27527
ageyrs:residPeriurban -0.005066 0.003557 -1.424 0.15476
ageyrs:residUrban -0.005046 0.003400 -1.484 0.13821
sexMale:residPeriurban 1.661961 1.367568 1.215 0.22468
sexMale:residUrban 1.452145 1.363439 1.065 0.28722
ageyrs:sexMale:residPeriurban -0.035862 0.031413 -1.142 0.25401
ageyrs:sexMale:residUrban -0.033653 0.031336 -1.074 0.28322
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1499 on 690 degrees of freedom
Multiple R-squared: 0.1184, Adjusted R-squared: 0.1044
F-statistic: 8.427 on 11 and 690 DF, p-value: 5.047e-14
And then plot the diagnostics
Code
<- par (mfrow = c (2 ,2 )).4 %>% plot (pch = 18 , cex= .5 )
Code
Next, we make a plot of the marginal effects after
Code
.4 <- ggeffects:: ggpredict (lm.4 , terms = c ("ageyrs" , "sex" , "resid" )).4 %>% plot () + labs (x = "Age in years" , y = "CCA thickness" , title = "Marginal relationship" )
There is a set of criteria for evaluating linear regression equations. These are:
There must be a linear relationship between the predictor and dependent variables
The residuals must be independent
Homoscedaticity: The variance of the residuals must be uniform at every level of x
The residual must be normally distributed
Code
<- %>% select (cca_0, ageyrs, whratio, totchol, ldl, sbp, dbp) %>% cor () %>% round (4 )%>% :: kbl (align = c (rep ("l" , 7 )), caption = "Correlation matrix" ) %>% :: kable_styling (bootstrap_options = c ("striped" , "bordered" , "condensed" , "hover" , "responsive" ), full_width= FALSE , html_font = "san_serif" , font_size = 16 )
Correlation matrix
cca_0
1.0000
0.3020
0.1398
0.1387
0.1131
0.1963
0.1538
ageyrs
0.3020
1.0000
0.2962
0.2196
0.1563
0.2755
0.1782
whratio
0.1398
0.2962
1.0000
0.1521
0.1247
0.1681
0.1509
totchol
0.1387
0.2196
0.1521
1.0000
0.9086
0.3198
0.2647
ldl
0.1131
0.1563
0.1247
0.9086
1.0000
0.2553
0.2069
sbp
0.1963
0.2755
0.1681
0.3198
0.2553
1.0000
0.7936
dbp
0.1538
0.1782
0.1509
0.2647
0.2069
0.7936
1.0000
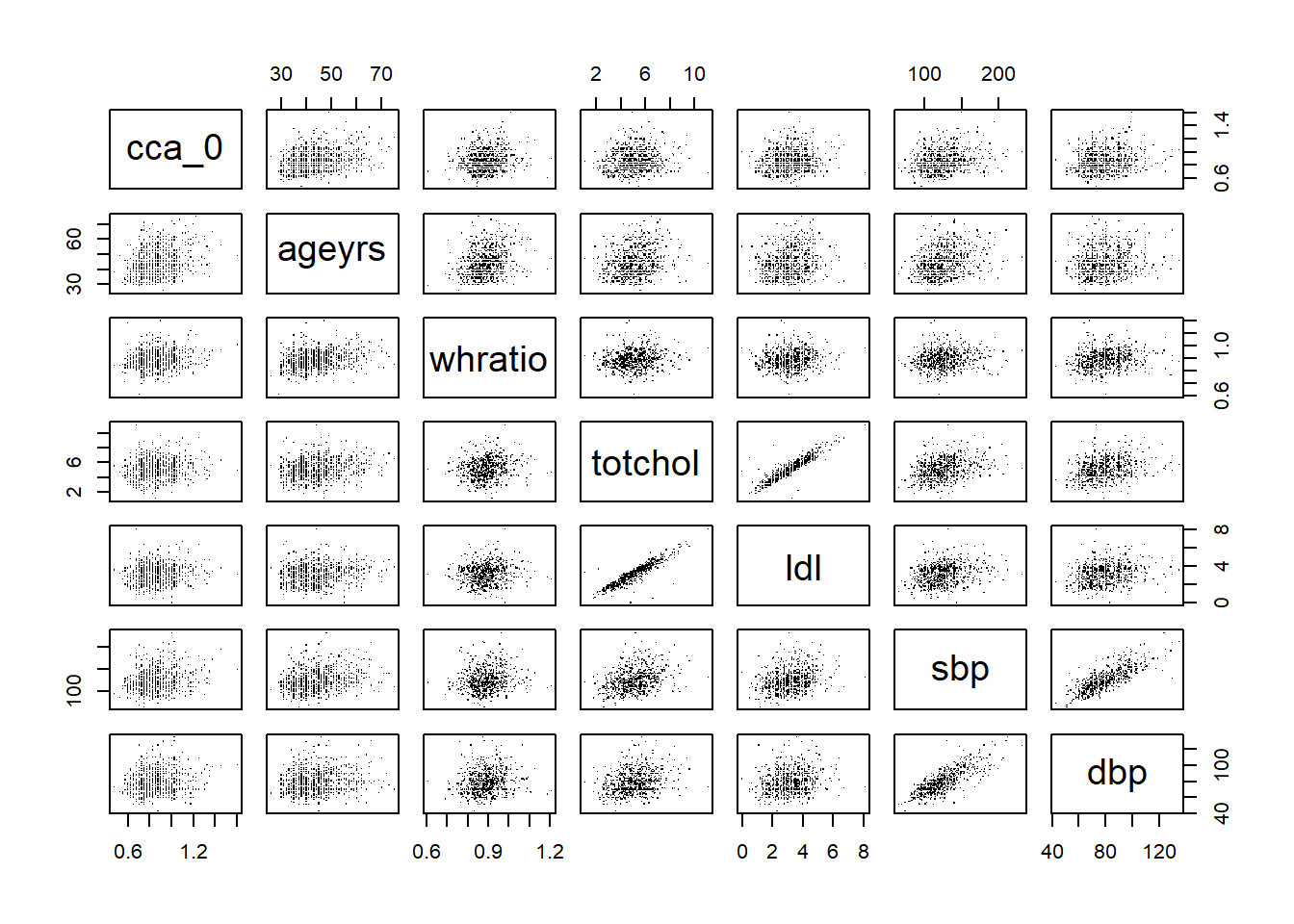
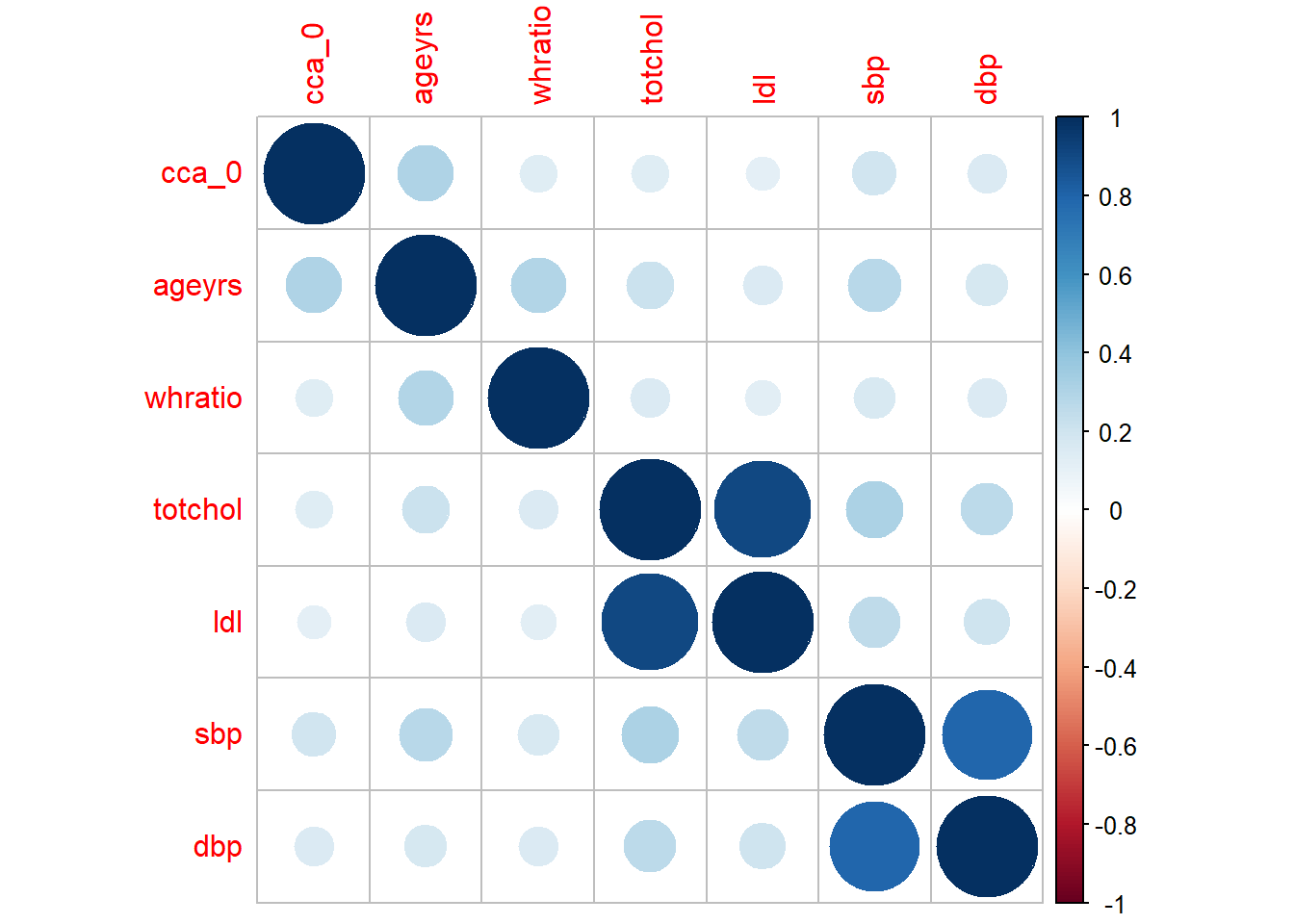
And then graphically present the correlation matrix
Code
%>% select (cca_0, ageyrs, whratio, totchol, ldl, sbp, dbp) %>% pairs (pch= "." )
Code
:: corrplot (corr.mat)
Both the correlation matrix and the diagram indicate a high correlation between
sbp and dbptotchol, ldl and hdl
These could potentially be indicative of multicollinearity
Fitting the model
We then fit the linear model and summarize it
Code
<- lm (cca_0 ~ sbp + dbp + ldl + ageyrs + totchol + whratio, data = dat)summary (lm1)
Call:
lm(formula = cca_0 ~ sbp + dbp + ldl + ageyrs + totchol + whratio,
data = dat)
Residuals:
Min 1Q Median 3Q Max
-0.33971 -0.10555 -0.01751 0.08800 0.68657
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.4697581 0.0744135 6.313 4.88e-10 ***
sbp 0.0006056 0.0004044 1.498 0.135
dbp 0.0002161 0.0006659 0.325 0.746
ldl 0.0021276 0.0129757 0.164 0.870
ageyrs 0.0044292 0.0006872 6.446 2.15e-10 ***
totchol 0.0035070 0.0104519 0.336 0.737
whratio 0.0895525 0.0839122 1.067 0.286
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1502 on 695 degrees of freedom
Multiple R-squared: 0.1086, Adjusted R-squared: 0.1009
F-statistic: 14.11 on 6 and 695 DF, p-value: 3.37e-15
The broom package gives us the opportunity of extracting the coefficient, residual, etc into a dataframe. We next do this below
Code
# A tibble: 7 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 0.470 0.0744 6.31 4.88e-10
2 sbp 0.000606 0.000404 1.50 1.35e- 1
3 dbp 0.000216 0.000666 0.325 7.46e- 1
4 ldl 0.00213 0.0130 0.164 8.70e- 1
5 ageyrs 0.00443 0.000687 6.45 2.15e-10
6 totchol 0.00351 0.0105 0.336 7.37e- 1
7 whratio 0.0896 0.0839 1.07 2.86e- 1
Code
# A tibble: 702 × 13
cca_0 sbp dbp ldl ageyrs totchol whratio .fitted .resid .hat .sigma
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.925 130 80 4.5 58 6.7 0.9 0.936 -0.0113 0.00677 0.150
2 0.975 120 80 2.3 48 4.4 0.924 0.875 0.0996 0.00359 0.150
3 0.85 110 80 1.3 40 2.7 0.877 0.822 0.0284 0.00730 0.150
4 0.875 120 80 3.5 38 5.1 0.869 0.831 0.0438 0.00301 0.150
5 1.6 150 100 3.1 49 4.9 1.01 0.913 0.687 0.00863 0.148
6 1.02 130 70 4.2 60 6.3 0.970 0.947 0.0777 0.00986 0.150
7 1 106 71 2.1 42 3.8 0.949 0.838 0.162 0.00503 0.150
8 1.32 130 100 3.2 55 4.9 0.843 0.913 0.412 0.0130 0.149
9 1.1 110 80 3.3 36 5.1 0.814 0.811 0.289 0.00503 0.150
10 1 110 70 0.7 55 3.3 0.912 0.890 0.110 0.0172 0.150
# ℹ 692 more rows
# ℹ 2 more variables: .cooksd <dbl>, .std.resid <dbl>
Code
# A tibble: 1 × 12
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.109 0.101 0.150 14.1 3.37e-15 6 338. -661. -624.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>
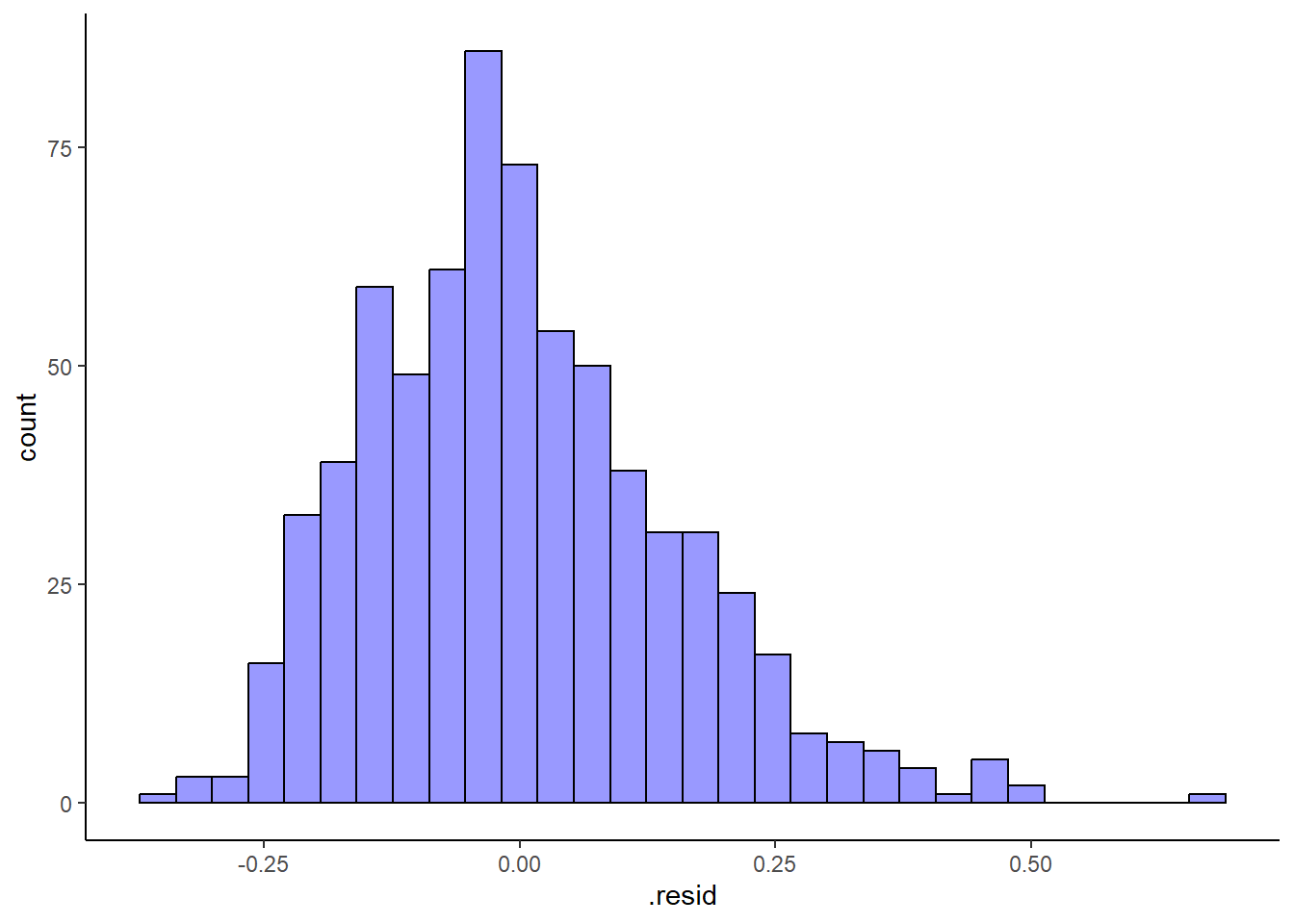
Code
%>% :: augment () %>% ggplot (aes (x= .resid)) + geom_histogram (fill = "blue" , col = "black" , alpha = .4 ) + theme_classic ()
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Code
%>% :: augment () %>% :: ggqqplot (x = ".resid" , col = "red" , title = "QQ plot of the residuals of the model" )
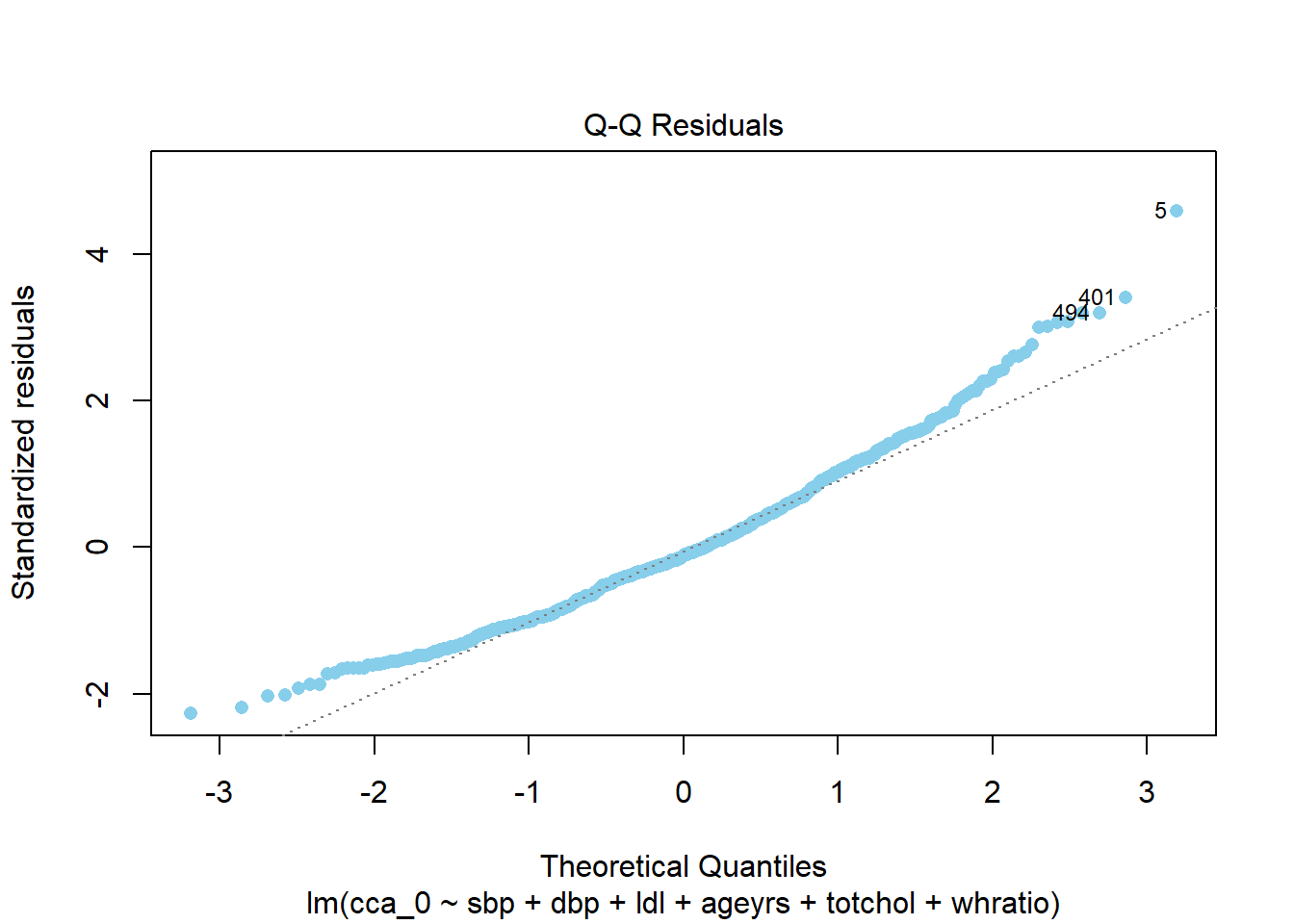
Code
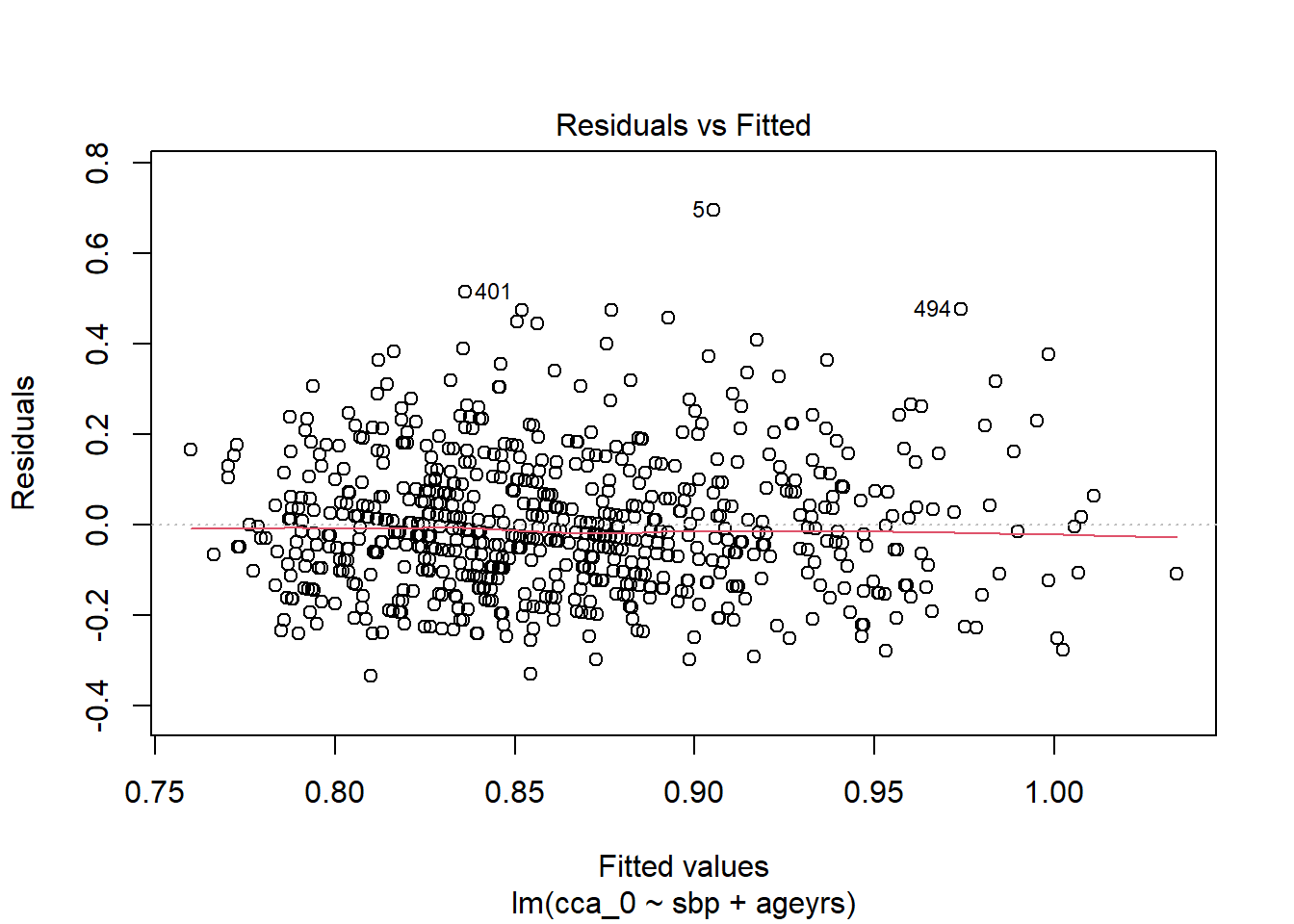
%>% plot (1 , pch = 16 , col = "skyblue" )
Code
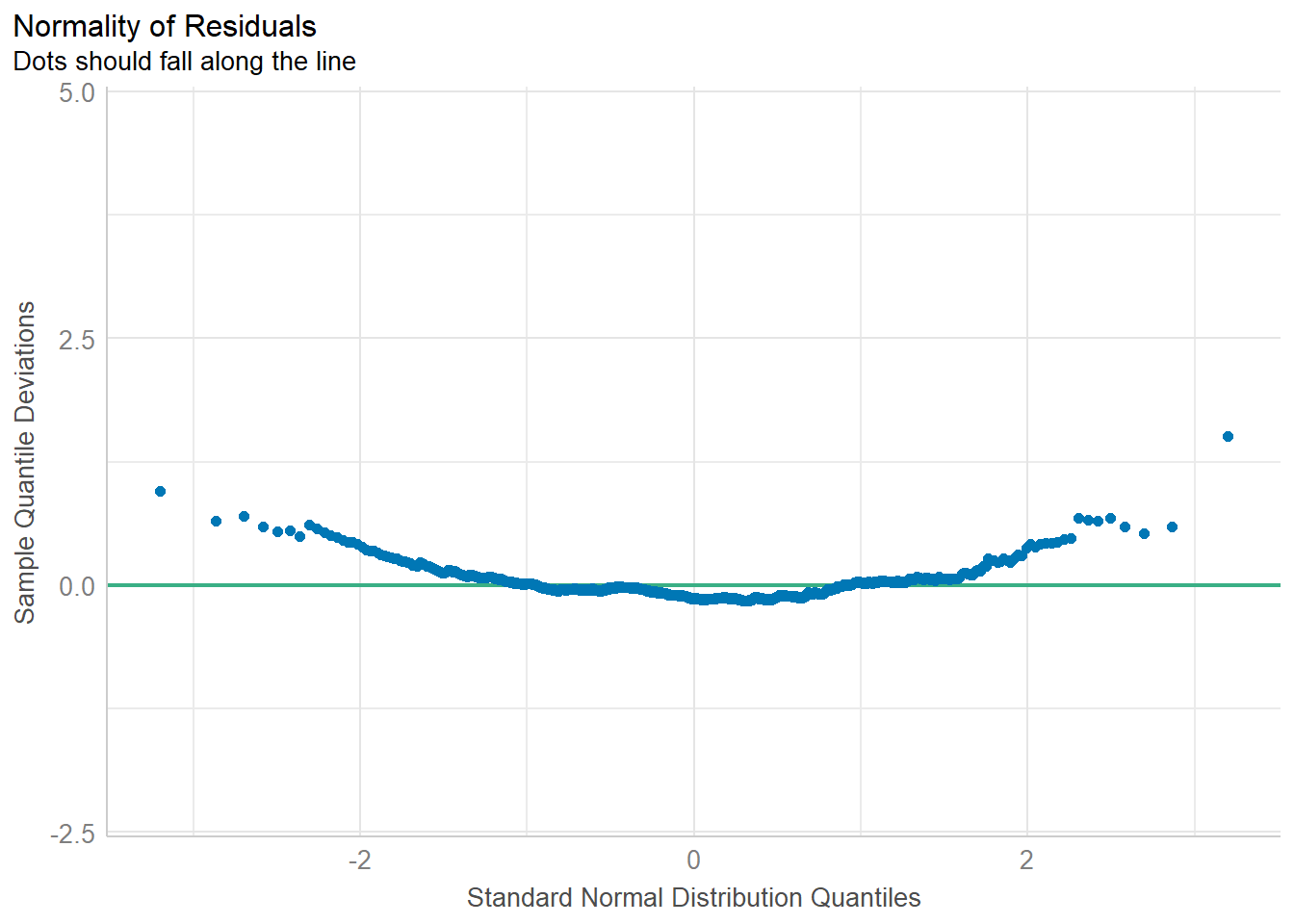
%>% plot (2 , pch = 16 , col = "skyblue" )
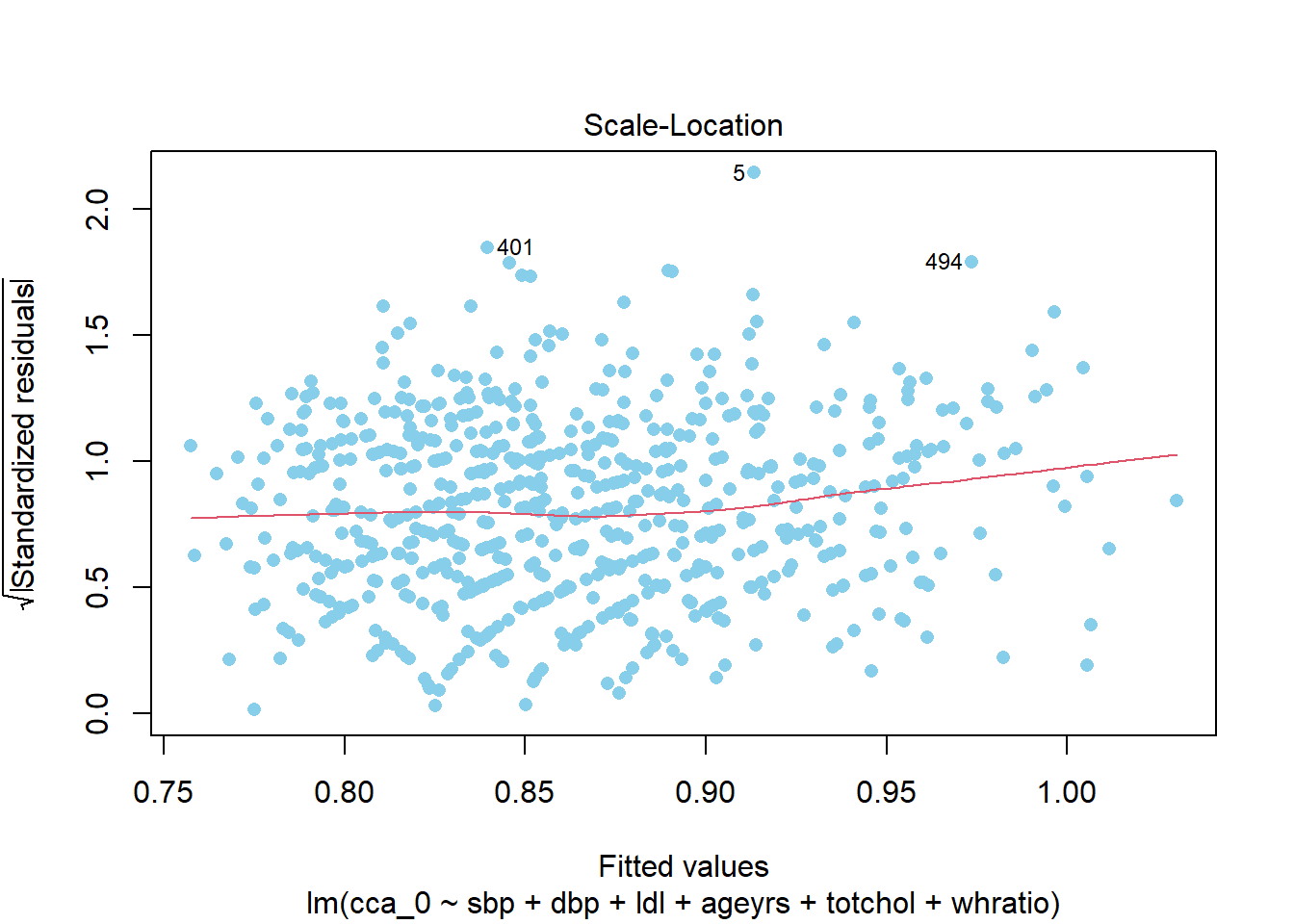
Code
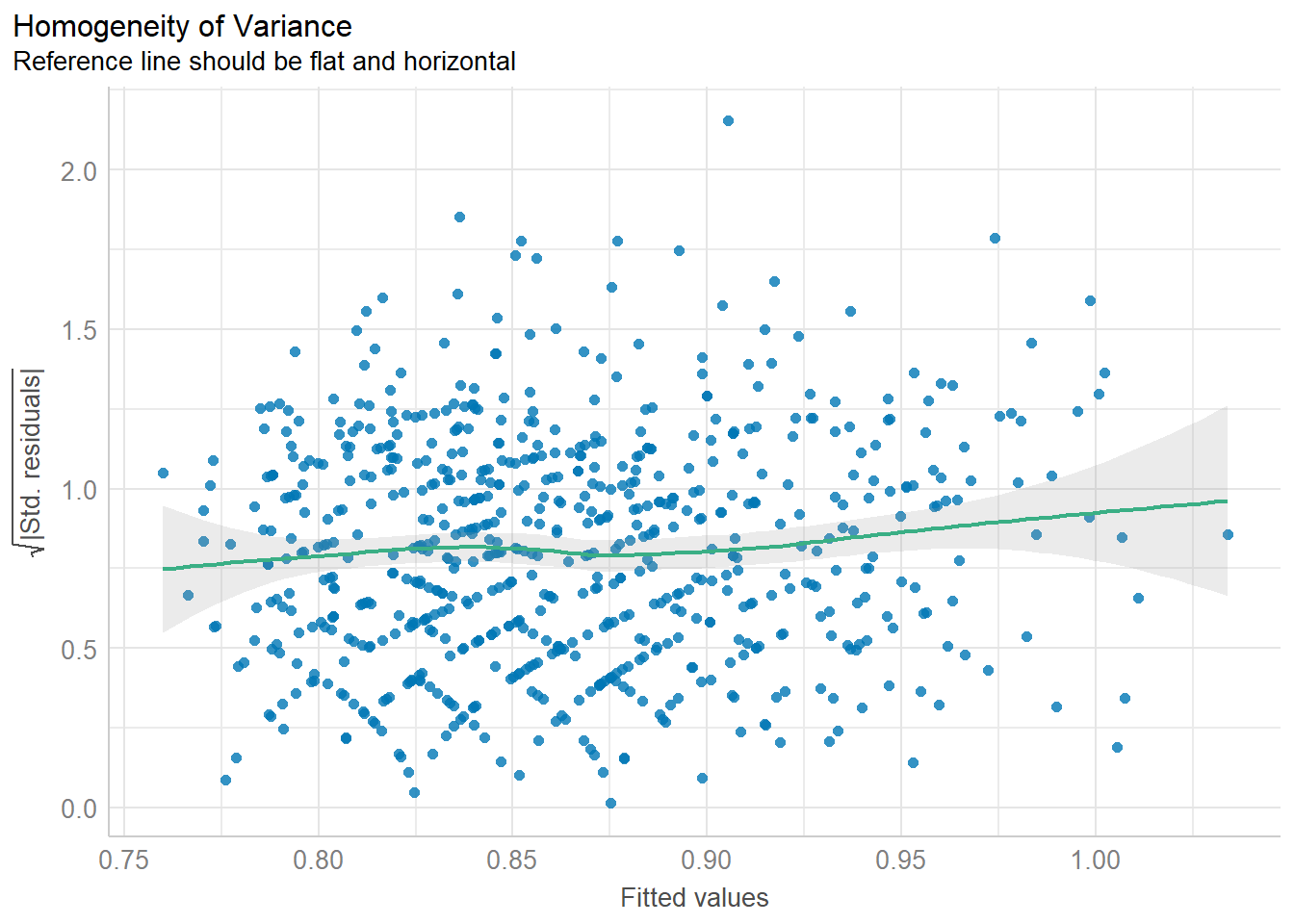
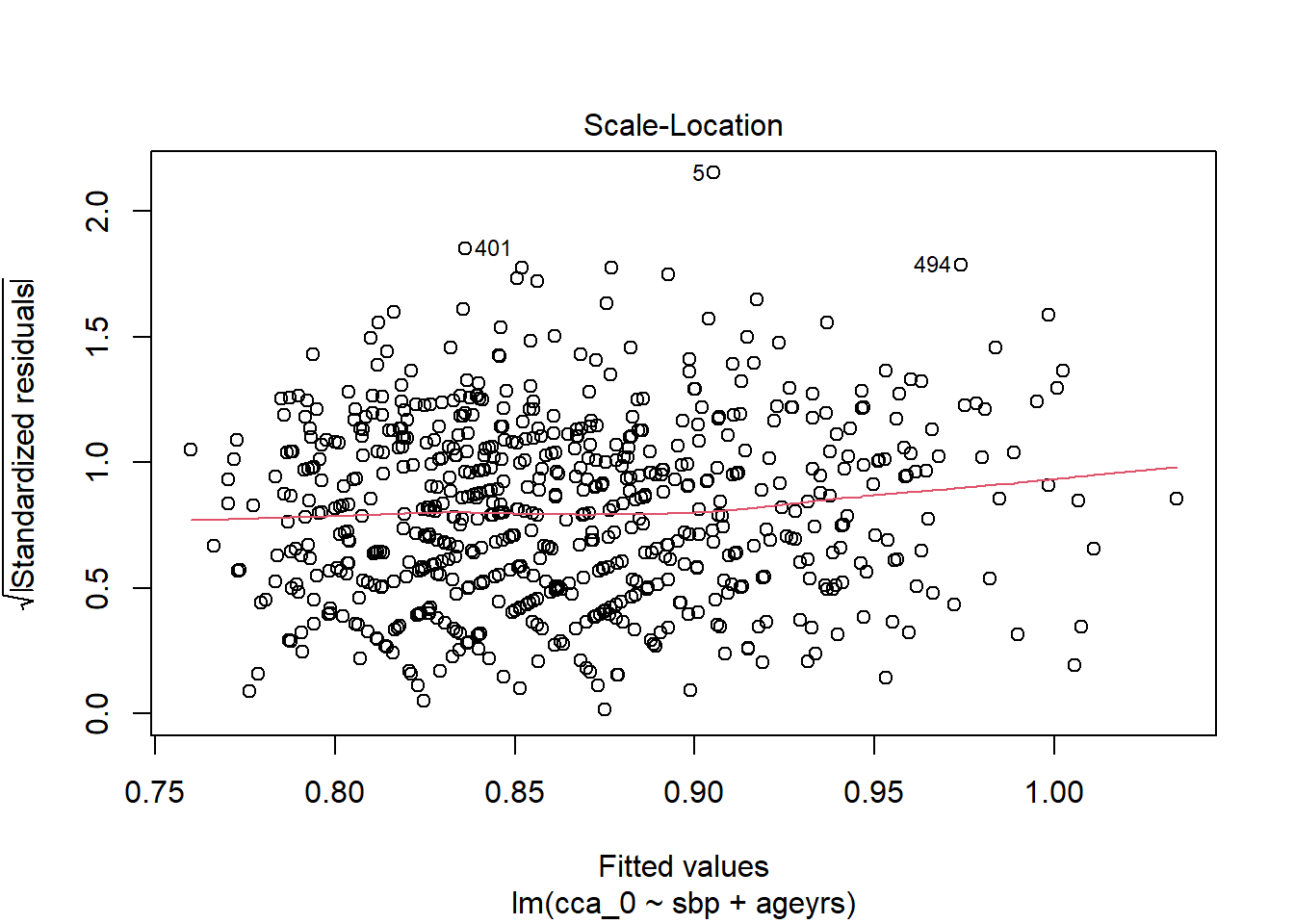
%>% plot (3 , pch = 16 , col = "skyblue" )
Code
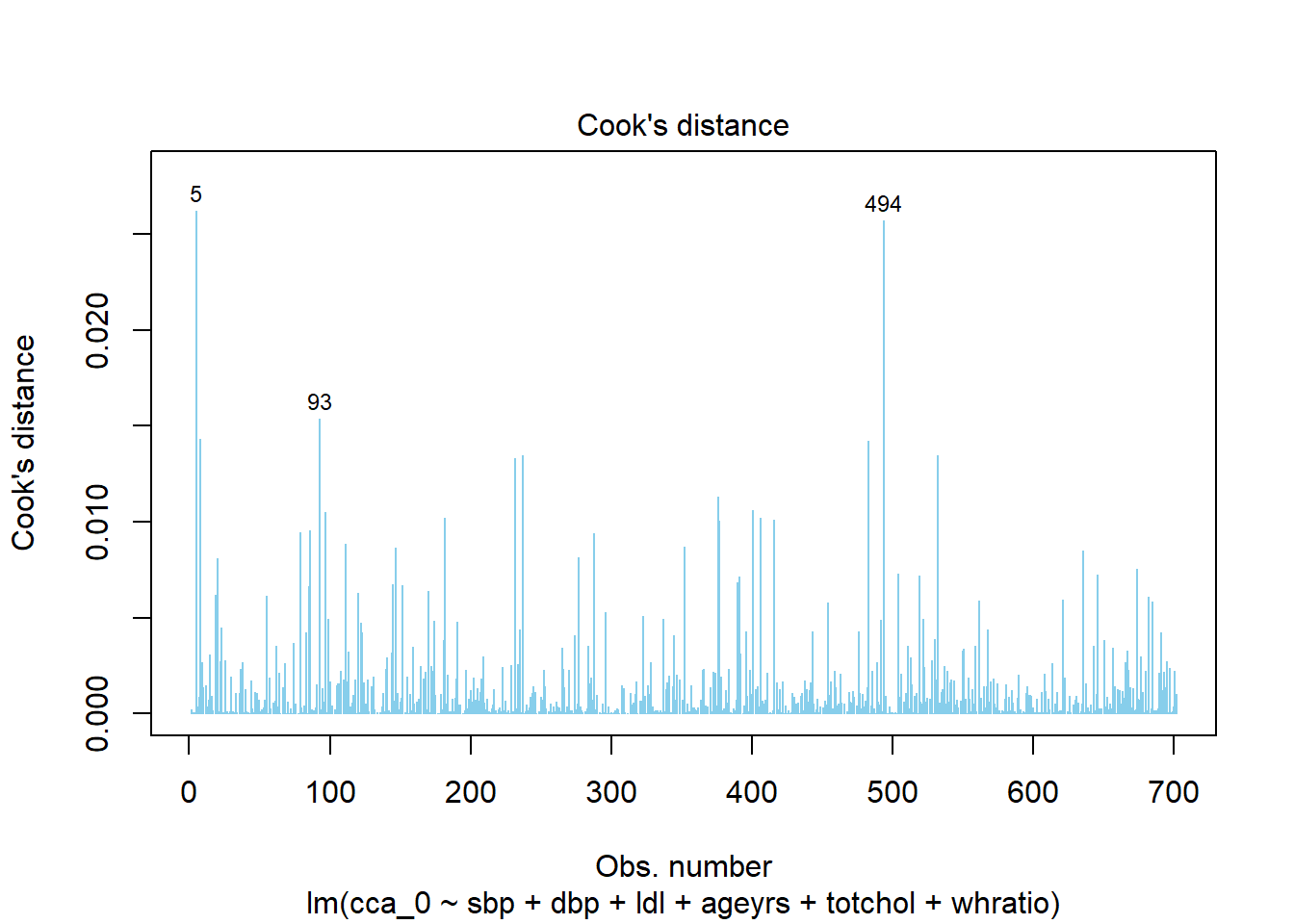
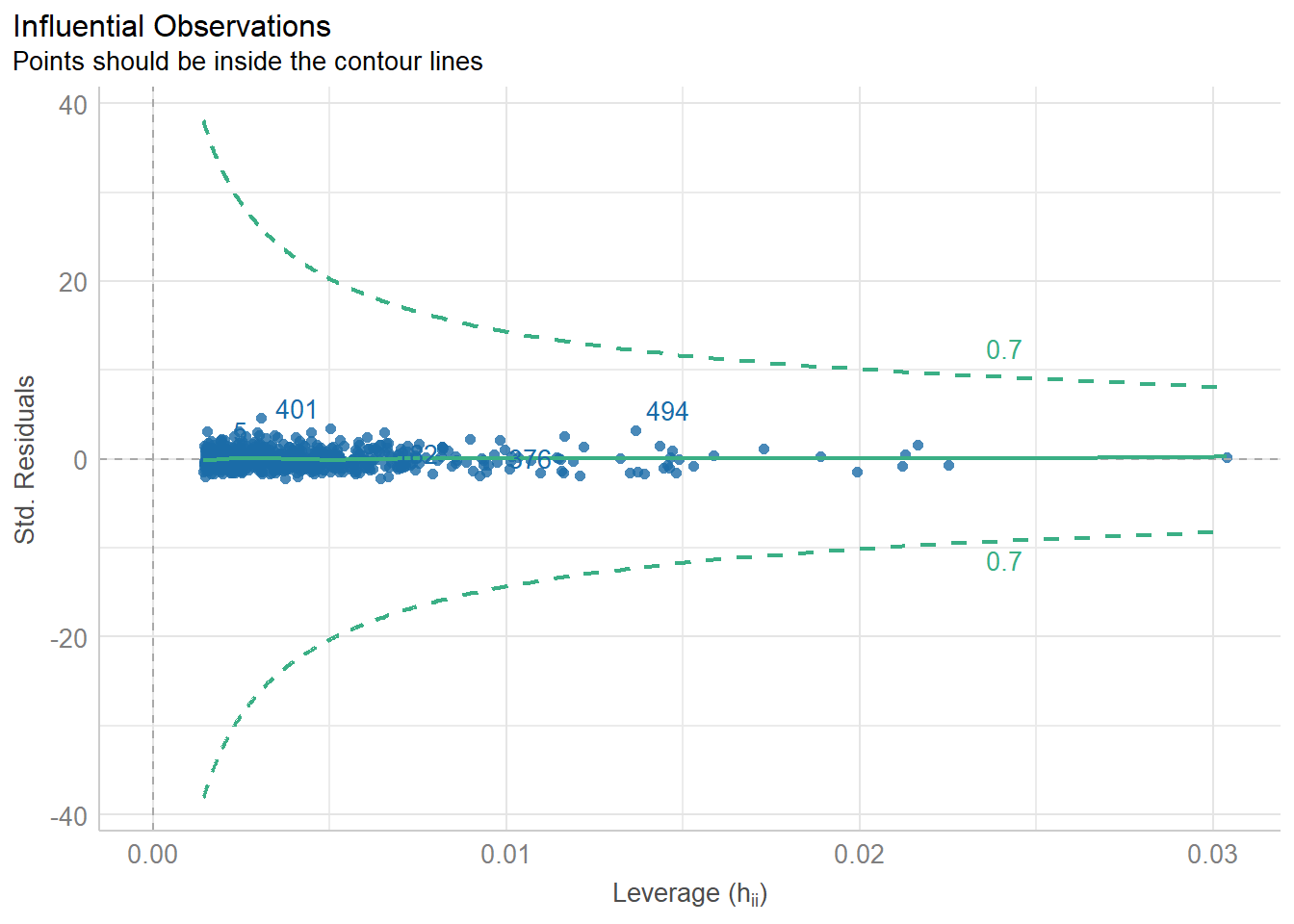
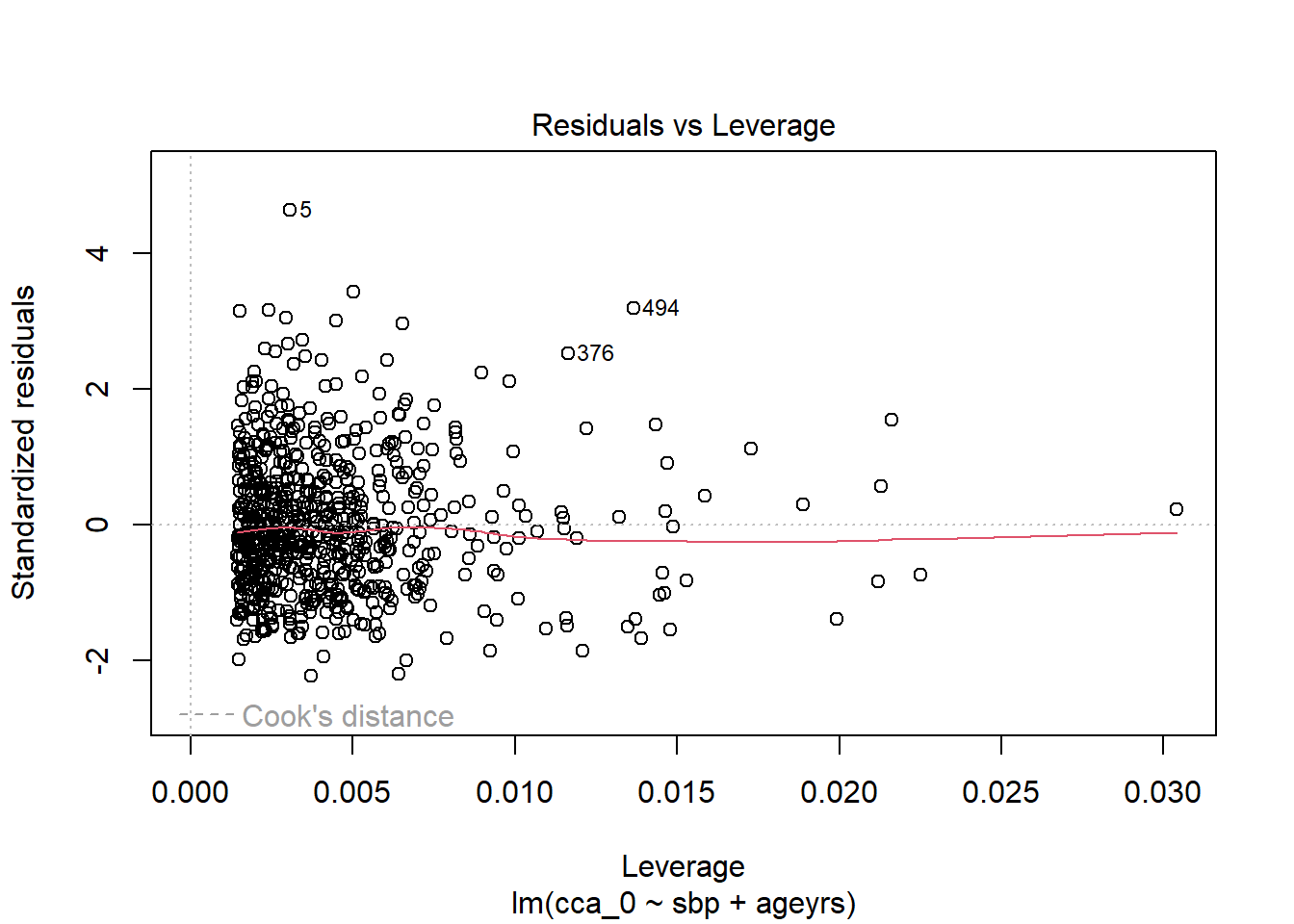
%>% plot (4 , pch = 16 , col = "skyblue" )
Checking multi-colinearity
Code
:: vif (lm1) %>% round (3 )
sbp dbp ldl ageyrs totchol whratio
2.914 2.725 5.829 1.198 6.155 1.114
Variable selection in multiple linear regression
Here we go through the drill of selecting the best model from a set of predictor variables. We do this with the help of the olsrr package.
Forward regression using the p-values for the selection of the best model
We begin by running the model as before
Code
<- lm (cca_0 ~ sbp + dbp + ldl + ageyrs + totchol + whratio, data = dat)summary (lm1)
Call:
lm(formula = cca_0 ~ sbp + dbp + ldl + ageyrs + totchol + whratio,
data = dat)
Residuals:
Min 1Q Median 3Q Max
-0.33971 -0.10555 -0.01751 0.08800 0.68657
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.4697581 0.0744135 6.313 4.88e-10 ***
sbp 0.0006056 0.0004044 1.498 0.135
dbp 0.0002161 0.0006659 0.325 0.746
ldl 0.0021276 0.0129757 0.164 0.870
ageyrs 0.0044292 0.0006872 6.446 2.15e-10 ***
totchol 0.0035070 0.0104519 0.336 0.737
whratio 0.0895525 0.0839122 1.067 0.286
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1502 on 695 degrees of freedom
Multiple R-squared: 0.1086, Adjusted R-squared: 0.1009
F-statistic: 14.11 on 6 and 695 DF, p-value: 3.37e-15
Next, we perform the forward stepwise selection using a cut-off p.value of 0.1. The table below gives a summary of the selection criteria
Code
<- olsrr:: ols_step_forward_p (lm1, penter= 0.1 )
Stepwise Summary
-----------------------------------------------------------------------------
Step Variable AIC SBC SBIC R2 Adj. R2
-----------------------------------------------------------------------------
0 Base Model -592.088 -582.980 -2584.497 0.00000 0.00000
1 ageyrs -657.220 -643.558 -2649.447 0.09120 0.08990
2 sbp -665.999 -647.783 -2658.153 0.10505 0.10249
3 totchol -665.472 -642.703 -2657.597 0.10692 0.10308
4 whratio -664.658 -637.334 -2656.749 0.10843 0.10331
-----------------------------------------------------------------------------
Final Model Output
------------------
Model Summary
----------------------------------------------------------------
R 0.329 RMSE 0.149
R-Squared 0.108 MSE 0.022
Adj. R-Squared 0.103 Coef. Var 17.374
Pred R-Squared 0.095 AIC -664.658
MAE 0.117 SBC -637.334
----------------------------------------------------------------
RMSE: Root Mean Square Error
MSE: Mean Square Error
MAE: Mean Absolute Error
AIC: Akaike Information Criteria
SBC: Schwarz Bayesian Criteria
ANOVA
--------------------------------------------------------------------
Sum of
Squares DF Mean Square F Sig.
--------------------------------------------------------------------
Regression 1.907 4 0.477 21.192 0.0000
Residual 15.676 697 0.022
Total 17.583 701
--------------------------------------------------------------------
Parameter Estimates
-------------------------------------------------------------------------------------
model Beta Std. Error Std. Beta t Sig lower upper
-------------------------------------------------------------------------------------
(Intercept) 0.473 0.073 6.461 0.000 0.330 0.617
ageyrs 0.004 0.001 0.251 6.461 0.000 0.003 0.006
sbp 0.001 0.000 0.106 2.742 0.006 0.000 0.001
totchol 0.005 0.004 0.043 1.132 0.258 -0.004 0.014
whratio 0.091 0.084 0.041 1.085 0.278 -0.073 0.255
-------------------------------------------------------------------------------------
The final best-fitting selected model is as below. However, I will run it on the standardized version of our variables as the coefficients are too small
Code
<- %>% mutate_at (c ("ageyrs" , "sbp" ), ~ (scale (.) %>% as.vector))<- lm (cca_0 ~ sbp + ageyrs, data = dat2)coefficients (lm.pval)
(Intercept) sbp ageyrs
0.86317664 0.01938752 0.04248649
Code
%>% flextable:: as_flextable ()
Estimate
Standard Error
t value
Pr(>|t|)
(Intercept)
0.863
0.006
152.427
0.0000
***
sbp
0.019
0.006
3.289
0.0011
**
ageyrs
0.042
0.006
7.207
0.0000
***
Signif. codes: 0 <= '***' < 0.001 < '**' < 0.01 < '*' < 0.05
Residual standard error: 0.15 on 699 degrees of freedom
Multiple R-squared: 0.105, Adjusted R-squared: 0.1025
F-statistic: 41.02 on 699 and 2 DF, p-value: 0.0000
Code
%>% :: tidy (conf.int= T) %>% mutate (across (estimate: conf.high,~ round (.x, 3 ))) %>% :: flextable () %>% :: font (i= 1 : 3 , fontname = "Times New Roman" ) %>% :: bold (i= 1 , j= 1 : 7 ,part = "header" ) %>% :: theme_zebra ()
term
estimate
std.error
statistic
p.value
conf.low
conf.high
(Intercept)
0.863
0.006
152.427
0.000
0.852
0.874
sbp
0.019
0.006
3.289
0.001
0.008
0.031
ageyrs
0.042
0.006
7.207
0.000
0.031
0.054
Code
%>% performance:: check_collinearity ()
# Check for Multicollinearity
Low Correlation
Term VIF VIF 95% CI Increased SE Tolerance Tolerance 95% CI
sbp 1.08 [1.03, 1.23] 1.04 0.92 [0.81, 0.97]
ageyrs 1.08 [1.03, 1.23] 1.04 0.92 [0.81, 0.97]
Code
%>% performance:: check_collinearity () %>% plot ()
Code
%>% performance:: check_heteroscedasticity ()
Warning: Heteroscedasticity (non-constant error variance) detected (p = 0.011).
Code
%>% performance:: check_heteroscedasticity () %>% plot ()
Code
%>% performance:: check_normality ()
Warning: Non-normality of residuals detected (p < .001).
Code
%>% performance:: check_normality () %>% plot ()
For confidence bands, please install `qqplotr`.
Code
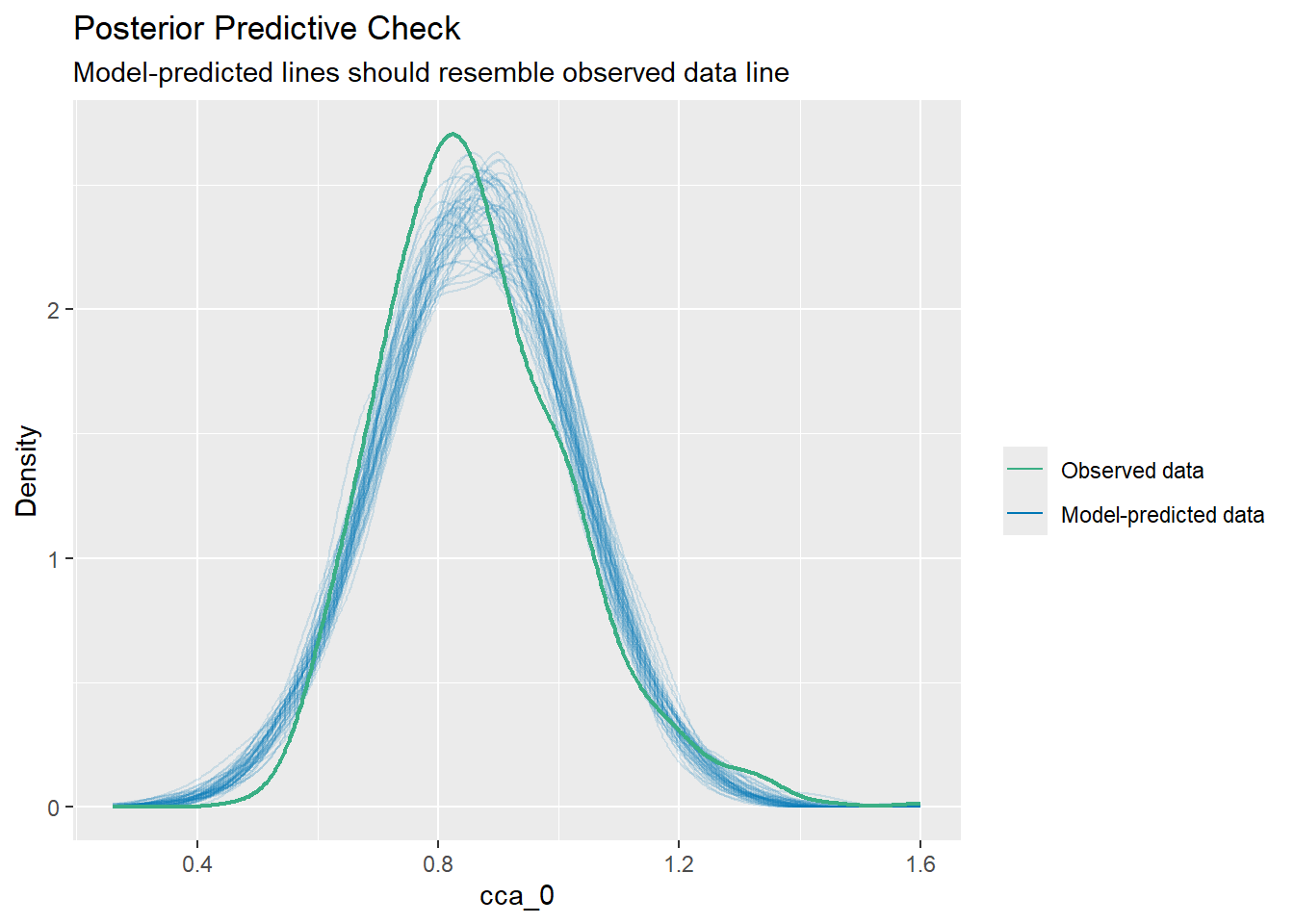
%>% performance:: check_predictions ()
Warning: Maximum value of original data is not included in the
replicated data.
Model may not capture the variation of the data.
Code
%>% performance:: check_predictions () %>% plot ()
Code
%>% performance:: check_outliers ()
OK: No outliers detected.
- Based on the following method and threshold: cook (0.8).
- For variable: (Whole model)
Code
%>% performance:: check_outliers () %>% plot ()
Code
Forward regression using the AIC for the selection of the best model
We change next to perform the forward stepwise selection using the AIC. The table below gives a summary of the selection criteria
Code
<- :: ols_step_forward_aic (lm1)
Stepwise Summary
-----------------------------------------------------------------------------
Step Variable AIC SBC SBIC R2 Adj. R2
-----------------------------------------------------------------------------
0 Base Model -592.088 -582.980 -2584.497 0.00000 0.00000
1 ageyrs -657.220 -643.558 -2649.447 0.09120 0.08990
2 sbp -665.999 -647.783 -2658.153 0.10505 0.10249
-----------------------------------------------------------------------------
Final Model Output
------------------
Model Summary
----------------------------------------------------------------
R 0.324 RMSE 0.150
R-Squared 0.105 MSE 0.022
Adj. R-Squared 0.102 Coef. Var 17.382
Pred R-Squared 0.097 AIC -665.999
MAE 0.117 SBC -647.783
----------------------------------------------------------------
RMSE: Root Mean Square Error
MSE: Mean Square Error
MAE: Mean Absolute Error
AIC: Akaike Information Criteria
SBC: Schwarz Bayesian Criteria
ANOVA
--------------------------------------------------------------------
Sum of
Squares DF Mean Square F Sig.
--------------------------------------------------------------------
Regression 1.847 2 0.924 41.023 0.0000
Residual 15.736 699 0.023
Total 17.583 701
--------------------------------------------------------------------
Parameter Estimates
-------------------------------------------------------------------------------------
model Beta Std. Error Std. Beta t Sig lower upper
-------------------------------------------------------------------------------------
(Intercept) 0.553 0.036 15.199 0.000 0.482 0.625
ageyrs 0.005 0.001 0.268 7.207 0.000 0.003 0.006
sbp 0.001 0.000 0.122 3.289 0.001 0.000 0.001
-------------------------------------------------------------------------------------
Code
Backward regression using the p.values for the selection of the best model
We change next to perform the backward stepwise removal using the p-value. The table below gives a summary of the selection criteria
Code
<- :: ols_step_backward_p (lm1, prem= 0.1 )
Stepwise Summary
-----------------------------------------------------------------------------
Step Variable AIC SBC SBIC R2 Adj. R2
-----------------------------------------------------------------------------
0 Full Model -660.788 -624.357 -2652.837 0.10860 0.10090
1 ldl -662.761 -630.883 -2654.831 0.10856 0.10216
2 dbp -664.658 -637.334 -2656.749 0.10843 0.10331
-----------------------------------------------------------------------------
Final Model Output
------------------
Model Summary
----------------------------------------------------------------
R 0.329 RMSE 0.149
R-Squared 0.108 MSE 0.022
Adj. R-Squared 0.103 Coef. Var 17.374
Pred R-Squared 0.095 AIC -664.658
MAE 0.117 SBC -637.334
----------------------------------------------------------------
RMSE: Root Mean Square Error
MSE: Mean Square Error
MAE: Mean Absolute Error
AIC: Akaike Information Criteria
SBC: Schwarz Bayesian Criteria
ANOVA
--------------------------------------------------------------------
Sum of
Squares DF Mean Square F Sig.
--------------------------------------------------------------------
Regression 1.907 4 0.477 21.192 0.0000
Residual 15.676 697 0.022
Total 17.583 701
--------------------------------------------------------------------
Parameter Estimates
-------------------------------------------------------------------------------------
model Beta Std. Error Std. Beta t Sig lower upper
-------------------------------------------------------------------------------------
(Intercept) 0.473 0.073 6.461 0.000 0.330 0.617
sbp 0.001 0.000 0.106 2.742 0.006 0.000 0.001
ageyrs 0.004 0.001 0.251 6.461 0.000 0.003 0.006
totchol 0.005 0.004 0.043 1.132 0.258 -0.004 0.014
whratio 0.091 0.084 0.041 1.085 0.278 -0.073 0.255
-------------------------------------------------------------------------------------
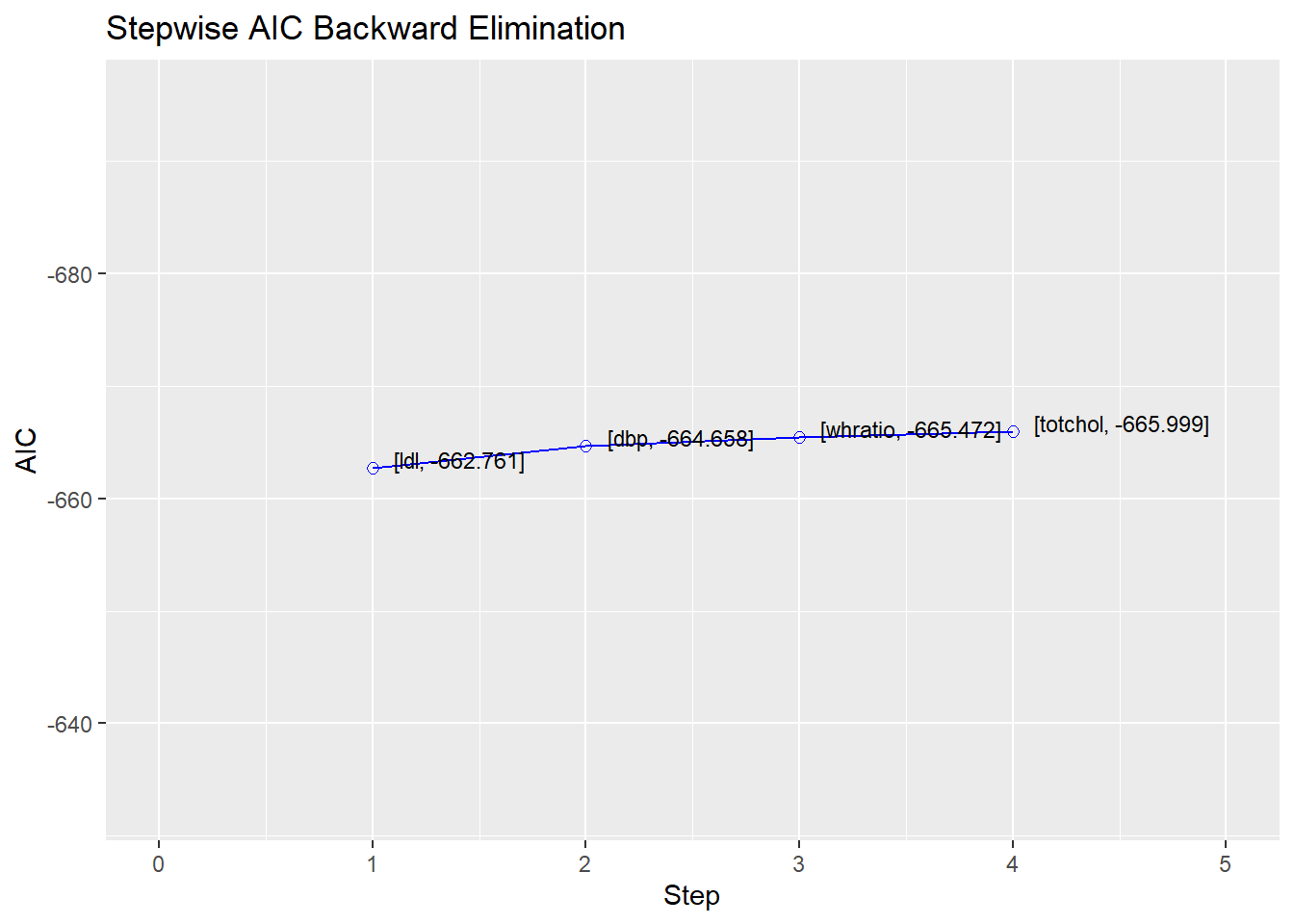
Backward regression using the aic for the selection of the best model
Code
<- :: ols_step_backward_aic (lm1)
Stepwise Summary
-----------------------------------------------------------------------------
Step Variable AIC SBC SBIC R2 Adj. R2
-----------------------------------------------------------------------------
0 Full Model -660.788 -624.357 -2652.837 0.10860 0.10090
1 ldl -662.761 -630.883 -2654.847 0.10856 0.10216
2 dbp -664.658 -637.334 -2656.776 0.10843 0.10331
3 whratio -665.472 -642.703 -2657.616 0.10692 0.10308
4 totchol -665.999 -647.783 -2658.163 0.10505 0.10249
-----------------------------------------------------------------------------
Final Model Output
------------------
Model Summary
----------------------------------------------------------------
R 0.324 RMSE 0.150
R-Squared 0.105 MSE 0.022
Adj. R-Squared 0.102 Coef. Var 17.382
Pred R-Squared 0.097 AIC -665.999
MAE 0.117 SBC -647.783
----------------------------------------------------------------
RMSE: Root Mean Square Error
MSE: Mean Square Error
MAE: Mean Absolute Error
AIC: Akaike Information Criteria
SBC: Schwarz Bayesian Criteria
ANOVA
--------------------------------------------------------------------
Sum of
Squares DF Mean Square F Sig.
--------------------------------------------------------------------
Regression 1.847 2 0.924 41.023 0.0000
Residual 15.736 699 0.023
Total 17.583 701
--------------------------------------------------------------------
Parameter Estimates
-------------------------------------------------------------------------------------
model Beta Std. Error Std. Beta t Sig lower upper
-------------------------------------------------------------------------------------
(Intercept) 0.553 0.036 15.199 0.000 0.482 0.625
sbp 0.001 0.000 0.122 3.289 0.001 0.000 0.001
ageyrs 0.005 0.001 0.268 7.207 0.000 0.003 0.006
-------------------------------------------------------------------------------------
Code
Both direction regression using the p.values for the selection of the best model
We change next to perform the backward stepwise removal using the p-value. The table below gives a summary of the selection criteria
Code
<- :: ols_step_both_p (prem = 0.1 , penter = 0.1 , progress = TRUE )
Stepwise Selection Method
-------------------------
Candidate Terms:
1. sbp
2. dbp
3. ldl
4. ageyrs
5. totchol
6. whratio
Variables Added/Removed:
=> ageyrs added
=> sbp added
No more variables to be added or removed.
Code
Stepwise Summary
-----------------------------------------------------------------------------
Step Variable AIC SBC SBIC R2 Adj. R2
-----------------------------------------------------------------------------
0 Base Model -592.088 -582.980 -2584.497 0.00000 0.00000
1 ageyrs (+) -657.220 -643.558 -2649.447 0.09120 0.08990
2 sbp (+) -665.999 -647.783 -2658.153 0.10505 0.10249
-----------------------------------------------------------------------------
Final Model Output
------------------
Model Summary
----------------------------------------------------------------
R 0.324 RMSE 0.150
R-Squared 0.105 MSE 0.022
Adj. R-Squared 0.102 Coef. Var 17.382
Pred R-Squared 0.097 AIC -665.999
MAE 0.117 SBC -647.783
----------------------------------------------------------------
RMSE: Root Mean Square Error
MSE: Mean Square Error
MAE: Mean Absolute Error
AIC: Akaike Information Criteria
SBC: Schwarz Bayesian Criteria
ANOVA
--------------------------------------------------------------------
Sum of
Squares DF Mean Square F Sig.
--------------------------------------------------------------------
Regression 1.847 2 0.924 41.023 0.0000
Residual 15.736 699 0.023
Total 17.583 701
--------------------------------------------------------------------
Parameter Estimates
-------------------------------------------------------------------------------------
model Beta Std. Error Std. Beta t Sig lower upper
-------------------------------------------------------------------------------------
(Intercept) 0.553 0.036 15.199 0.000 0.482 0.625
ageyrs 0.005 0.001 0.268 7.207 0.000 0.003 0.006
sbp 0.001 0.000 0.122 3.289 0.001 0.000 0.001
-------------------------------------------------------------------------------------
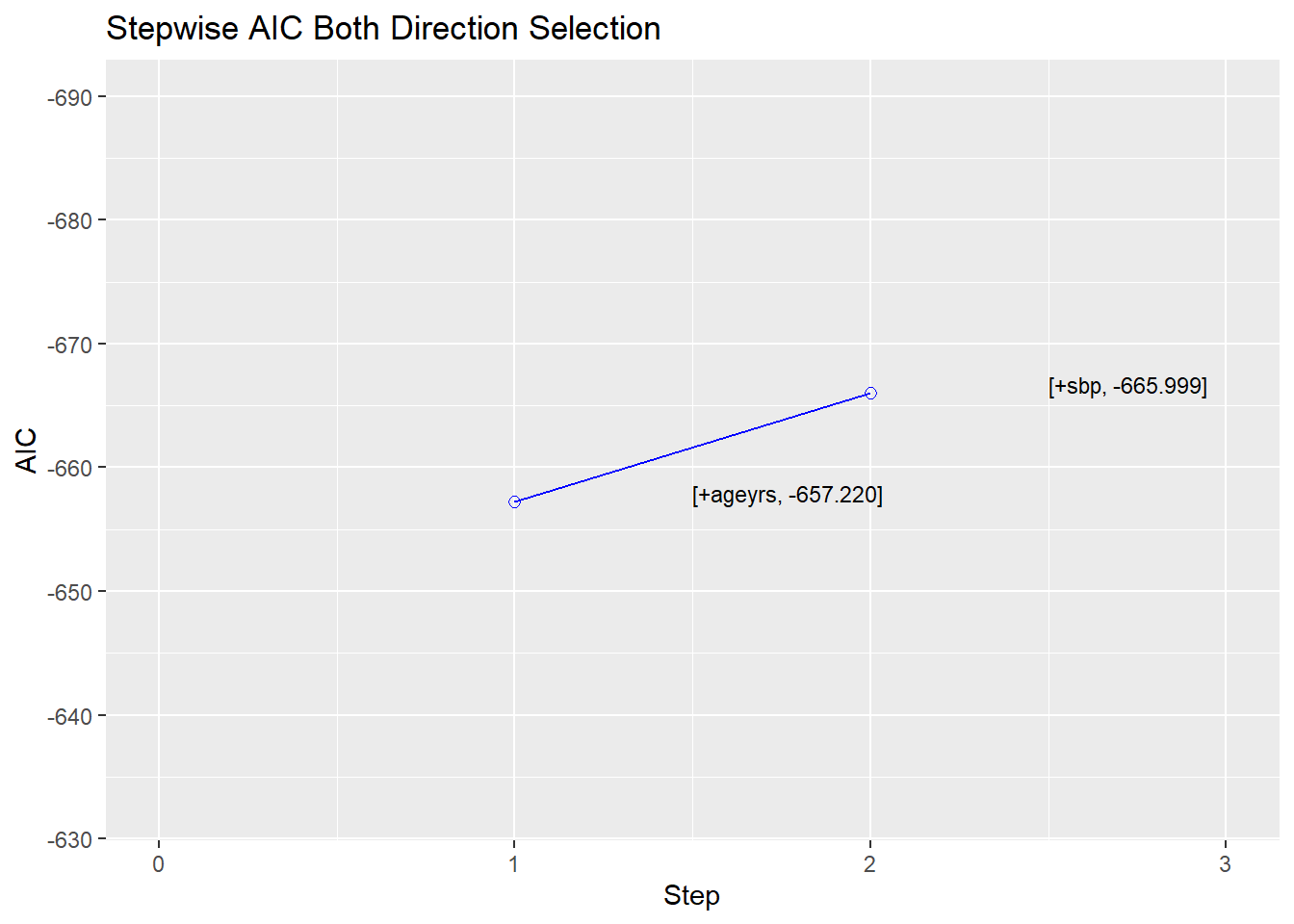
Both direction regression using the aic for the selection of the best model
Code
<- :: ols_step_both_aic (lm1, progress = TRUE )
Stepwise Selection Method
-------------------------
Candidate Terms:
1. sbp
2. dbp
3. ldl
4. ageyrs
5. totchol
6. whratio
Variables Added/Removed:
=> ageyrs added
=> sbp added
No more variables to be added or removed.
Code
Stepwise Summary
-----------------------------------------------------------------------------
Step Variable AIC SBC SBIC R2 Adj. R2
-----------------------------------------------------------------------------
0 Base Model -592.088 -582.980 -2584.497 0.00000 0.00000
1 ageyrs (+) -657.220 -643.558 -2649.447 0.09120 0.08990
2 sbp (+) -665.999 -647.783 -2658.153 0.10505 0.10249
-----------------------------------------------------------------------------
Final Model Output
------------------
Model Summary
----------------------------------------------------------------
R 0.324 RMSE 0.150
R-Squared 0.105 MSE 0.022
Adj. R-Squared 0.102 Coef. Var 17.382
Pred R-Squared 0.097 AIC -665.999
MAE 0.117 SBC -647.783
----------------------------------------------------------------
RMSE: Root Mean Square Error
MSE: Mean Square Error
MAE: Mean Absolute Error
AIC: Akaike Information Criteria
SBC: Schwarz Bayesian Criteria
ANOVA
--------------------------------------------------------------------
Sum of
Squares DF Mean Square F Sig.
--------------------------------------------------------------------
Regression 1.847 2 0.924 41.023 0.0000
Residual 15.736 699 0.023
Total 17.583 701
--------------------------------------------------------------------
Parameter Estimates
-------------------------------------------------------------------------------------
model Beta Std. Error Std. Beta t Sig lower upper
-------------------------------------------------------------------------------------
(Intercept) 0.553 0.036 15.199 0.000 0.482 0.625
ageyrs 0.005 0.001 0.268 7.207 0.000 0.003 0.006
sbp 0.001 0.000 0.122 3.289 0.001 0.000 0.001
-------------------------------------------------------------------------------------
Code
Pick the best predicting model.
The output below is divided into two tables. The first picks out the best 1, 2, 3, etc predictir model. Hence the best 3 predictor model for our linear regression is sbp ageyrs totchol. However, to pick the best model out of the lot, in case 6, we look at the second table. The best will have a high R-Square Adj.R-Square and Pred R-Square. Also, the best model will give the lower C(p), AIC, SBIC, SBC, MSEP, FPE, HSP, and APC. Looking at our output it appears the best will be the 2 predictor mode of lm(cca_0 ~ ageyrs + sbp).
Code
<- :: ols_step_best_subset (lm1)
Best Subsets Regression
-------------------------------------------------
Model Index Predictors
-------------------------------------------------
1 ageyrs
2 sbp ageyrs
3 sbp ageyrs totchol
4 sbp ageyrs totchol whratio
5 sbp dbp ageyrs totchol whratio
6 sbp dbp ldl ageyrs totchol whratio
-------------------------------------------------
Subsets Regression Summary
-------------------------------------------------------------------------------------------------------------------------------------
Adj. Pred
Model R-Square R-Square R-Square C(p) AIC SBIC SBC MSEP FPE HSP APC
-------------------------------------------------------------------------------------------------------------------------------------
1 0.0912 0.0899 0.0858 10.5636 -657.2199 -2649.4469 -643.5581 16.0250 0.0229 0.0000 0.9140
2 0.1050 0.1025 0.0968 1.7667 -665.9991 -2658.1525 -647.7834 15.8035 0.0226 0.0000 0.9026
3 0.1069 0.1031 0.0961 2.3041 -665.4722 -2657.5966 -642.7025 15.7930 0.0226 0.0000 0.9033
4 0.1084 0.1033 0.0952 3.1292 -664.6577 -2656.7487 -637.3341 15.7890 0.0227 0.0000 0.9044
5 0.1086 0.1022 0.0929 5.0269 -662.7610 -2654.8305 -630.8835 15.8093 0.0227 0.0000 0.9068
6 0.1086 0.1009 0.0912 7.0000 -660.7882 -2652.8371 -624.3567 15.8315 0.0228 0.0000 0.9094
-------------------------------------------------------------------------------------------------------------------------------------
AIC: Akaike Information Criteria
SBIC: Sawa's Bayesian Information Criteria
SBC: Schwarz Bayesian Criteria
MSEP: Estimated error of prediction, assuming multivariate normality
FPE: Final Prediction Error
HSP: Hocking's Sp
APC: Amemiya Prediction Criteria